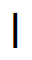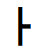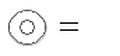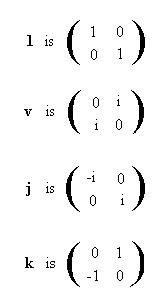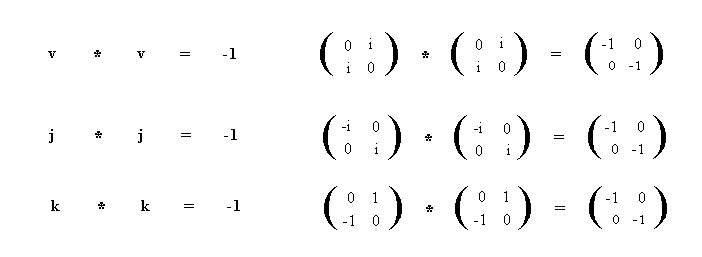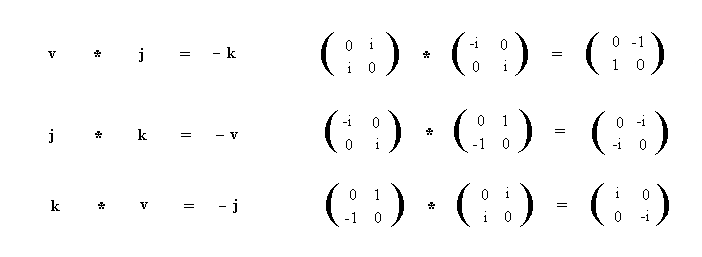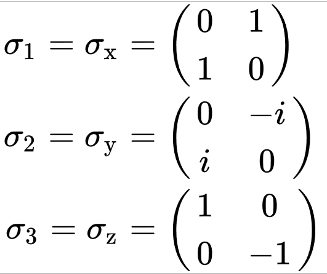Copyright Jere Northrop August, 2021
Table of Contents
Introduction
Chapters
Appendix B Science
Appendix C Maximum Entropy
Notes and References
Chapters
- Origins
- Relational Symmetries, derivation and description
- The Relational Science Model.
Appendix B Science
Appendix C Maximum Entropy
Notes and References
The Relational Symmetry Paradigm
Introduction
..This proposal is a response to a number of problems that are facing us today. These stem from concerns that our rising human population may have already exceeded what our planet can sustainably support, and that this is driving derivative problems of Climate Change, global pandemics, and environmental pollution. While we have the scientific and technical knowledge to resolve these problems we are not implementing this knowledge because of a series of unresolved social problems.
This is not a call to make you aware of these problems, but rather to offer a possible solution to them. The rationale and context for the proposed solutions are described in the following two quotations.
Albert Einstein: A new type of thinking is essential if mankind is to survive and move toward higher levels. (1)
Buckminster Fuller: If you want to teach people a new way of thinking, don’t bother trying to teach them. Instead, give them a tool, the use of which will lead to new ways of thinking. (2)
As a tool the existing scientific paradigm is unquestionably the most impressive human achievement to date. It comprises a series of models that, taken together, provide us with an unprecedented ability to predict events in the world we live in, and construct technologies and machines that make our lives easier. However, these models are not always philosophically compatible or consistent with each other, and they do not adequately address the roots of our current problems.
A possible way to resolve these difficulties is to expand the foundational presumptions of modern science to include consciousness and language. To do this look for the patterns in recorded history and our own personal experiences that are consistent with science and mathematics. These patterns can be formulated as Relational Symmetries. When they are expressed symbolically they might provide the desired tool for a new way of thinking. However, to do this they will also have to fully explain the verified successes of modern science.
In the Relational Symmetry Paradigm a Relational Symmetry is defined as a one-three fourness symbolic formalism that is based on the assumption that understanding is relational, and that there are four fundamental types of relations; self relation, linear relation, relational relation, and interrelational relation.
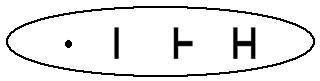
Here are four signs that represent a Relational Symmetry:
This is not a call to make you aware of these problems, but rather to offer a possible solution to them. The rationale and context for the proposed solutions are described in the following two quotations.
Albert Einstein: A new type of thinking is essential if mankind is to survive and move toward higher levels. (1)
Buckminster Fuller: If you want to teach people a new way of thinking, don’t bother trying to teach them. Instead, give them a tool, the use of which will lead to new ways of thinking. (2)
As a tool the existing scientific paradigm is unquestionably the most impressive human achievement to date. It comprises a series of models that, taken together, provide us with an unprecedented ability to predict events in the world we live in, and construct technologies and machines that make our lives easier. However, these models are not always philosophically compatible or consistent with each other, and they do not adequately address the roots of our current problems.
A possible way to resolve these difficulties is to expand the foundational presumptions of modern science to include consciousness and language. To do this look for the patterns in recorded history and our own personal experiences that are consistent with science and mathematics. These patterns can be formulated as Relational Symmetries. When they are expressed symbolically they might provide the desired tool for a new way of thinking. However, to do this they will also have to fully explain the verified successes of modern science.
In the Relational Symmetry Paradigm a Relational Symmetry is defined as a one-three fourness symbolic formalism that is based on the assumption that understanding is relational, and that there are four fundamental types of relations; self relation, linear relation, relational relation, and interrelational relation.
Here are four signs that represent a Relational Symmetry:
Here are four additional signs that also represent a Relational Symmetry. They can be viewed as an evolution of the first four signs.
These eight signs are foundational presumptions and hence precede definition. Their meaning will evolve through example and use. An initial example as to how these map into our experience considers...
...representing a point, line, surface, and volume. Then...
...maps into boundary, crossing a boundary, labelling or marking what you are doing (language), and then interrelating various things you have done in various ways.
We know that to be credible the Relational Symmetry Paradigm must show that the incorporation of consciousness and language into the foundations of science has to be consistent with all the experiential successes of physics, and that specifically means that this has to include both General Relativity and Quantum Mechanics, two models that are presently philosophically incompatible with each other. The argument here is that the...
formalism is symmetrical with the mathematical quaternion that is used extensively in quantum mechanics, and which is also compatible with the tensor formulation of general relativity. A potential unification of Quantum Mechanics and General Relativity is proposed by casting space-time itself as a Relational Symmetry quaternion.
The Relational Symmetry Paradigm further assumes that thermodynamic entropy is identical to informational entropy so that the Maximum Entropy Principle is symmetrical in physical, chemical, and biological phenomena. Similarly, charge, spin, and mass – energy are viewed as symmetrical with sex, right and left handedness, and consciousness – language. The wave particle duality in physics is also viewed as being symmetrical to the mind body problem in philosophy, and both are isomorphic to and resolved by the primary Relational Symmetries shown above. In this way we see evidence for the new paradigm in our own personal experience, the natural world we live in, and the technologies that we have created. We don’t have to understand the scientific complexities to effectively use these simple symbolic formalisms. Being aware of the symmetries and how they are manifested in our experiences is enough. It is easy and it works.
This document will describe the origin and evolution of the Relational Symmetries. It will show how they are manifested in straightforward principles that are simple and have been in our common knowledge for years. These include:
The Golden Rule; Do unto others as you would have others do unto you.
“We hold these truths to be self evident, That all people are created equal. That they are endowed by their Creator with certain inalienable Rights, that among these are Life, Liberty and the Pursuit of Happiness”.
Ethical principles such as: Help others when possible and do no harm; All persons have intrinsic and unconditional worth; Tell the Truth; Justice is the fair, equitable, and appropriate distribution of resources.
All these resonate and are consistent with the Relational Symmetries.
This proposal will not try to change your beliefs or the way you think. That you have to do yourself. However, if you are concerned about the problems referenced above, and do not know what you can realistically do about resolving them, then you might want to consider the ideas presented here. These might be the tools that can indeed result in a new way of thinking.
To Summarize:
The Relational Symmetry Paradigm is a tool that has been developed from history, our own personal experiences, and science to help us understand how to live a peaceful cooperative existence with each other and the planet. To use this tool we have to;
Covariantly communicate with each other.
Honestly disclose what we really believe.
Not tell lies.
If we fail to do this, in science or politics, we may end up living on an increasingly unrecognizable and dangerous planet, or dying in a world that no longer supports life as we know it.
This document will describe the origin and evolution of the Relational Symmetries. It will show how they are manifested in straightforward principles that are simple and have been in our common knowledge for years. These include:
The Golden Rule; Do unto others as you would have others do unto you.
“We hold these truths to be self evident, That all people are created equal. That they are endowed by their Creator with certain inalienable Rights, that among these are Life, Liberty and the Pursuit of Happiness”.
Ethical principles such as: Help others when possible and do no harm; All persons have intrinsic and unconditional worth; Tell the Truth; Justice is the fair, equitable, and appropriate distribution of resources.
All these resonate and are consistent with the Relational Symmetries.
This proposal will not try to change your beliefs or the way you think. That you have to do yourself. However, if you are concerned about the problems referenced above, and do not know what you can realistically do about resolving them, then you might want to consider the ideas presented here. These might be the tools that can indeed result in a new way of thinking.
To Summarize:
The Relational Symmetry Paradigm is a tool that has been developed from history, our own personal experiences, and science to help us understand how to live a peaceful cooperative existence with each other and the planet. To use this tool we have to;
Covariantly communicate with each other.
Honestly disclose what we really believe.
Not tell lies.
If we fail to do this, in science or politics, we may end up living on an increasingly unrecognizable and dangerous planet, or dying in a world that no longer supports life as we know it.
Chapter 1
Origins
The Relational Symmetry Paradigm has evolved over many years as a way to build an understanding of ourselves and the environment and universe that we inhabit. The goal is that this will be a tool that will help us effectively use both our own personal experience and the incredible wisdom and knowledge that has been accumulated by our global society over the course of human history. The sheer size and complexity of all this information makes it extremely difficult to categorize and learn so that it can be readily available for use in our everyday lives.
The Relational Symmetries comprise a structure and a process that may help us resolve this situation. First recognize that we are very complex entities and that we live in a very complex universe. So, to avoid making this tool also very complex, and hence difficult to understand and use effectively, choose a path of simplification and abstraction. Do this with the realization that while it will be an approximation of very complex phenomena it still could elucidate a few essential features that recur fractal-like throughout the perceived complexity we experience. This will make it easier to understand and use.
Begin with what we know best, and where we have the most direct experience – ourselves. This chapter will focus on this approach, with the further assumption that if these symbolic abstractions, the Relational Symmetries, are valid for me, that they will also be valid for you. Thus they will be invariant and unchanged for each of us. We will both agree that this is consistent with how we understand ourselves and our environment.
Let’s start by examining areas or subjects where we do agree.
We both have a mind.
We both have a body.
We use language.
We live in a world that is external to our minds and bodies.
Expanding on this.
Our mind is a consciousness with;
Desires and needs.
It experiences emotions and feelings.
It remembers.
Our bodies have a physical structure that is made of matter;
Bodies can move, act.
They experience sensations, see things, hear things, touch and taste and smell things.
They also can make things, create things. change things.
We communicate and think with words that are part of a language.
The language comprises signs which may be represented by symbols or sounds.
The signs have definitions, how they are described relative to other signs.
They may be associated with images.
They can be combined to form and represent ideas.
Finally we exist and live within an external reality, something outside of our bodies, an environment, a world, a universe.
There are other things, outside of ourselves in this world.
Things can interact with other things, experience forces, move.
Things have characteristic properties, shapes, colors, size, textures.
They are all connected. They are connected to us.
The Relational Symmetry Paradigm is generated from universal relational symmetries that are extractable from the archetypal concepts that are presented above. These relational symmetries can be abstracted into simple tools, symbolic formalisms that will allow us to see comparable symmetries in all aspects of the universe, including those that are expressed in the existing operational paradigms of science, religion, and politics.
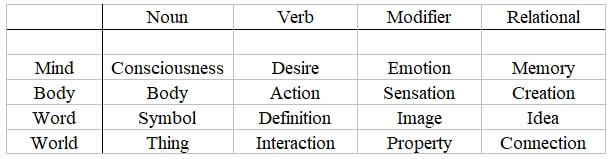
Because this new paradigm is used with and described by language, we can organize it in terms of the structure of language itself, that is, in terms of words that are nouns, verbs, modifiers, and relationals (words that are connectives, articles, prepositions, etc.). Here is a diagram that illustrates how the shared agreements and beliefs previously described, can be grouped and presented to illustrate the symmetries that constitute this new way of thinking.
The Relational Symmetry Paradigm has evolved over many years as a way to build an understanding of ourselves and the environment and universe that we inhabit. The goal is that this will be a tool that will help us effectively use both our own personal experience and the incredible wisdom and knowledge that has been accumulated by our global society over the course of human history. The sheer size and complexity of all this information makes it extremely difficult to categorize and learn so that it can be readily available for use in our everyday lives.
The Relational Symmetries comprise a structure and a process that may help us resolve this situation. First recognize that we are very complex entities and that we live in a very complex universe. So, to avoid making this tool also very complex, and hence difficult to understand and use effectively, choose a path of simplification and abstraction. Do this with the realization that while it will be an approximation of very complex phenomena it still could elucidate a few essential features that recur fractal-like throughout the perceived complexity we experience. This will make it easier to understand and use.
Begin with what we know best, and where we have the most direct experience – ourselves. This chapter will focus on this approach, with the further assumption that if these symbolic abstractions, the Relational Symmetries, are valid for me, that they will also be valid for you. Thus they will be invariant and unchanged for each of us. We will both agree that this is consistent with how we understand ourselves and our environment.
Let’s start by examining areas or subjects where we do agree.
We both have a mind.
We both have a body.
We use language.
We live in a world that is external to our minds and bodies.
Expanding on this.
Our mind is a consciousness with;
Desires and needs.
It experiences emotions and feelings.
It remembers.
Our bodies have a physical structure that is made of matter;
Bodies can move, act.
They experience sensations, see things, hear things, touch and taste and smell things.
They also can make things, create things. change things.
We communicate and think with words that are part of a language.
The language comprises signs which may be represented by symbols or sounds.
The signs have definitions, how they are described relative to other signs.
They may be associated with images.
They can be combined to form and represent ideas.
Finally we exist and live within an external reality, something outside of our bodies, an environment, a world, a universe.
There are other things, outside of ourselves in this world.
Things can interact with other things, experience forces, move.
Things have characteristic properties, shapes, colors, size, textures.
They are all connected. They are connected to us.
The Relational Symmetry Paradigm is generated from universal relational symmetries that are extractable from the archetypal concepts that are presented above. These relational symmetries can be abstracted into simple tools, symbolic formalisms that will allow us to see comparable symmetries in all aspects of the universe, including those that are expressed in the existing operational paradigms of science, religion, and politics.
Because this new paradigm is used with and described by language, we can organize it in terms of the structure of language itself, that is, in terms of words that are nouns, verbs, modifiers, and relationals (words that are connectives, articles, prepositions, etc.). Here is a diagram that illustrates how the shared agreements and beliefs previously described, can be grouped and presented to illustrate the symmetries that constitute this new way of thinking.
Generally I do not expect that there were any disagreements with this, with the possible exception of the last idea of connection. Connectivity may be understood in different ways. In one view we are all composed of matter, which is not conscious, but which does interact with, and hence is connected to, all of the other matter in the universe. This may occur via gravitational and electromagnetic forces. In another view we as conscious entities are connected to a superior consciousness, a God, which in turn is connected to all of the rest of the universe. In a third view we as conscious entities are connected to our immediate environment and to all the other conscious entities who have currently and historically communicated with us. In all of these views we are connected, but in different ways.
The tool-like nature of the Relational Symmetry Paradigm is primarily designed to be a very simple way to help us think and understand. Once it becomes familiar it should provide a platform and protocol for the understanding and derivation of the models that are currently used in science, religion, and politics. By unifying the paradigms underlying these models this new way of thinking may provide insights that will enable us to resolve the major problems identified at the beginning of this document.
The tool-like nature of the Relational Symmetry Paradigm is primarily designed to be a very simple way to help us think and understand. Once it becomes familiar it should provide a platform and protocol for the understanding and derivation of the models that are currently used in science, religion, and politics. By unifying the paradigms underlying these models this new way of thinking may provide insights that will enable us to resolve the major problems identified at the beginning of this document.
Chapter 2
Relational Symmetries
Here is a description of how the Relational Symmetries comprise a very simple but sophisticated procedure that can make thinking
and communicating easier. It is based on the assumption that understanding is relational, and that there are four fundamental types
of relations; self relation, linear relation, relational relation, and interrelational relation. These reflect an archetypal fractal
symmetry underlying both our own consciousness and the universe itself.
This symmetry comprises a one-three fourness structure and we can recognize it in many phenomena we normally think of as having four dimensions or characteristics. They include:
The view of the universe according to early Greek philosophers as comprising earth, fire, water, and air. Earth as a solid and the fluids (fire, water, and air).
Our normal view of space-time as comprising time measured with clocks, and space measured with rulers, (length, width, and height).
Color: white and three primary colors, (red, yellow, and blue). These can be reflected as black with (orange, green, and purple).
Music: The key of C, the white keys on a piano, can be represented as a combination of two four note chords with a key note followed by three resonating additional notes, C major seventh (C, E, G, and B), and D minor seventh (D, F, A, and C).
Grammar: the parts of speech are nouns which are connected with; verbs, modifiers, and relational words.
There are four types of numbers. The counting numbers (integers) that are then used to form fractions (rational numbers), transcendental or exponential numbers (real numbers), and numbers incorporating the square root of minus one (complex numbers).
The four forces of physics; where gravitation joins the electromagnetic, weak nuclear, and strong nuclear interactions to explain motion.
Chemistry where the photon as an energy packet with a wave particle duality interacts with three subatomic particles, the electron, proton, and neutron.
The scientific method where a hypothesis is formed, tested by experiment, the results are analyzed, and either a new modified hypothesis is then formed or the results are recorded as part of the evidence supporting the original hypothesis.
This is like a rational thinker using deductive, inductive, and abductive processes to understand a subject.
From these examples of phenomena with a one-three fourness structure we can construct specific symbolic formalisms which define the concept of Relational Symmetry. These formalisms are themselves examples of the Relational Symmetry structure that they represent.
Here are four signs that represent the initial symbolic formalism of a symmetrical relational structure.
Here is a description of how the Relational Symmetries comprise a very simple but sophisticated procedure that can make thinking
and communicating easier. It is based on the assumption that understanding is relational, and that there are four fundamental types
of relations; self relation, linear relation, relational relation, and interrelational relation. These reflect an archetypal fractal
symmetry underlying both our own consciousness and the universe itself.
This symmetry comprises a one-three fourness structure and we can recognize it in many phenomena we normally think of as having four dimensions or characteristics. They include:
The view of the universe according to early Greek philosophers as comprising earth, fire, water, and air. Earth as a solid and the fluids (fire, water, and air).
Our normal view of space-time as comprising time measured with clocks, and space measured with rulers, (length, width, and height).
Color: white and three primary colors, (red, yellow, and blue). These can be reflected as black with (orange, green, and purple).
Music: The key of C, the white keys on a piano, can be represented as a combination of two four note chords with a key note followed by three resonating additional notes, C major seventh (C, E, G, and B), and D minor seventh (D, F, A, and C).
Grammar: the parts of speech are nouns which are connected with; verbs, modifiers, and relational words.
There are four types of numbers. The counting numbers (integers) that are then used to form fractions (rational numbers), transcendental or exponential numbers (real numbers), and numbers incorporating the square root of minus one (complex numbers).
The four forces of physics; where gravitation joins the electromagnetic, weak nuclear, and strong nuclear interactions to explain motion.
Chemistry where the photon as an energy packet with a wave particle duality interacts with three subatomic particles, the electron, proton, and neutron.
The scientific method where a hypothesis is formed, tested by experiment, the results are analyzed, and either a new modified hypothesis is then formed or the results are recorded as part of the evidence supporting the original hypothesis.
This is like a rational thinker using deductive, inductive, and abductive processes to understand a subject.
From these examples of phenomena with a one-three fourness structure we can construct specific symbolic formalisms which define the concept of Relational Symmetry. These formalisms are themselves examples of the Relational Symmetry structure that they represent.
Here are four signs that represent the initial symbolic formalism of a symmetrical relational structure.
These are reflected to generate a second symmetrical relational structure.
Finally these are combined to form the Relational Symmetry Paradigm.
To develop an understanding of how to use the Relational Symmetries we start by considering these signs as undefined presumptions. We will build meaning for them through illustration and their use.
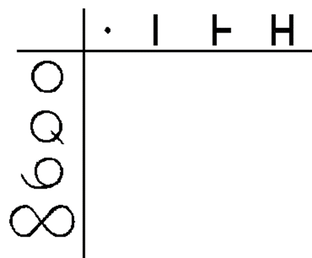
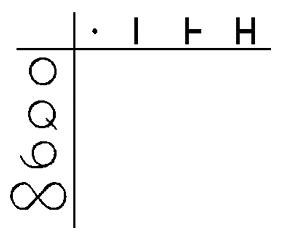
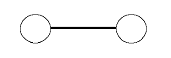
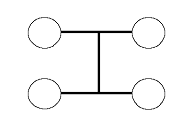
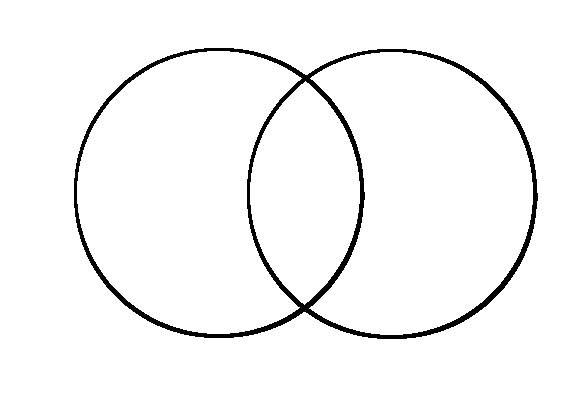
The first example of how to assign meaning to the Relational Symmetry formalisms comes from Relational Systems Theory, which was developed by Jon Ray Hamann in the late 1960s and early 1970s (3). Let circles represent systems and lines represent relations. Then...
The first example of how to assign meaning to the Relational Symmetry formalisms comes from Relational Systems Theory, which was developed by Jon Ray Hamann in the late 1960s and early 1970s (3). Let circles represent systems and lines represent relations. Then...
Looking at just the relations in the Relational Systems formalism shows that they are isomorphic with the primary Relational Symmetry of...
The initial and primary meanings which can then be assigned to the first four initial signs are;
This becomes the first Relational Symmetry. It is crucial to understand that these are each independent concepts. Thus a linear relation is an entity in and of itself, and is not a line comprised of an indeterminable number of points. Similarly a relational relation cannot be fully described as a combination of linear relations but must be viewed more as a surface, a fundamentally different concept. We can symbolically represent this concept with a diagram that comprises two lines that connect, or an indeterminant number of lines, but these are only illustrations.
A similar argument also applies to the interrelational relation. This represents a concept symmetrical to a space or volume which can be illustrated by three lines. However, it is an independent concept and not one that is composed of three or an indefinite number of lines or surfaces.
Presenting the self relational concept as a system also presents the opportunity and necessity for additional levels of symmetry. This requires that we make a distinction or boundary to specify what is part of a system and what is not. The boundary defines the self relational nature of the system, what distinguishes the system from the rest of the universe. This then generates the second level of relational symmetries that are in a one to one correspondence with the first level. Call these symbols the second relational symmetry. Symbols used to represent this second level symmetry are;
A similar argument also applies to the interrelational relation. This represents a concept symmetrical to a space or volume which can be illustrated by three lines. However, it is an independent concept and not one that is composed of three or an indefinite number of lines or surfaces.
Presenting the self relational concept as a system also presents the opportunity and necessity for additional levels of symmetry. This requires that we make a distinction or boundary to specify what is part of a system and what is not. The boundary defines the self relational nature of the system, what distinguishes the system from the rest of the universe. This then generates the second level of relational symmetries that are in a one to one correspondence with the first level. Call these symbols the second relational symmetry. Symbols used to represent this second level symmetry are;
In the secondary Relational Symmetry the first symbol is represented as a distinction, a recognition that something is different from something else. The next symbol shows that things that are distinct from each other can also be related to each other by crossing a boundary. The third symbol shows that other boundaries or distinctions can be created, expressed symbolically, and related to the original distinguished things so that we call tell them apart. The last symbol shows that further relations can be made between previously distinguished things by creating additional relations between their symbolically distinguished symbols.
These examples of meaning are;
These examples of meaning are;
Finally there is a need for a way to interconnect all of these symbolic constructs and their conjoined meanings with each other.
The interpretation of self relation as both a point and a boundary introduces additional symbolic formalisms that encompass how the Relational Symmetries themselves can be combined into units that represent the concepts of particles and organizations, both from a structural and a process perspective.
When the initial self relational sign, a point, is reflected as a circle, a boundary, it can be expanded to include the other initial three signs in the one-three fourness symmetry.
When the initial self relational sign, a point, is reflected as a circle, a boundary, it can be expanded to include the other initial three signs in the one-three fourness symmetry.
This generates a concept of particle or organization and this can be applied to our own beliefs and how they can be implemented in categorical, procedural, or governmental forms. For example, consider these symmetrical interpretations;
Our basic beliefs.
The methodologies we use for each of them.
How they have been institutionalized in the three branches of the US government.
All these descriptions show how the Relational Symmetries comprise a very simple but sophisticated procedure that can make thinking and communicating easier. They are based on the assumption that understanding is relational, and that consideration of all four fundamental types of relations; self relation, linear relation, relational relation, and interrelational relation, are necessary to gain a full understanding of anything. This reflects an archetypal fractal symmetry that is a recurring pattern that underlies both our own consciousness and the universe itself.
As we proceed in generalizing the Relational Symmetry Paradigm, the process we will use will utilize the first Relational Symmetry, as follows.
Pick a subject. Look at it from the perspective of how it is comprised by and of the four fundamental types of relations.
What is the concept.
How is it manifested in our experience, expressed in what we do, performed in our movements and actions.
Create a description of this concept and what we are doing with it. This will usually involve writing but may include any form of symbolic expression such as sculpture, music, poetry, drawing, painting, dance, theater, or other forms of personal or artistic expression.
Finally evaluate what we have done, how does this compare with other subjects and our engagement with them from this relational perspective. How does this become knitted into our very being, a part of who we are.
This process itself is an example of the first relational symmetry.
Our basic beliefs.
The methodologies we use for each of them.
How they have been institutionalized in the three branches of the US government.
All these descriptions show how the Relational Symmetries comprise a very simple but sophisticated procedure that can make thinking and communicating easier. They are based on the assumption that understanding is relational, and that consideration of all four fundamental types of relations; self relation, linear relation, relational relation, and interrelational relation, are necessary to gain a full understanding of anything. This reflects an archetypal fractal symmetry that is a recurring pattern that underlies both our own consciousness and the universe itself.
As we proceed in generalizing the Relational Symmetry Paradigm, the process we will use will utilize the first Relational Symmetry, as follows.
Pick a subject. Look at it from the perspective of how it is comprised by and of the four fundamental types of relations.
What is the concept.
How is it manifested in our experience, expressed in what we do, performed in our movements and actions.
Create a description of this concept and what we are doing with it. This will usually involve writing but may include any form of symbolic expression such as sculpture, music, poetry, drawing, painting, dance, theater, or other forms of personal or artistic expression.
Finally evaluate what we have done, how does this compare with other subjects and our engagement with them from this relational perspective. How does this become knitted into our very being, a part of who we are.
This process itself is an example of the first relational symmetry.
As we repeat this process these signs and the concepts they represent will be reflected, extended, and combined in many different ways. Eventually they will become helpful in understanding the complexities of our lives and the universe within which we live.
The Relational Paradigm itself is fractal-like in that the relational symmetries repeat in every aspect or element of ourselves as well as the universe. Thus it comprises multiple levels of representation. The most critical of these is how they coalesce into the new paradigm. This is most concisely represented as;
The Relational Paradigm itself is fractal-like in that the relational symmetries repeat in every aspect or element of ourselves as well as the universe. Thus it comprises multiple levels of representation. The most critical of these is how they coalesce into the new paradigm. This is most concisely represented as;
To illustrate how this is used look back at what we agreed upon in Chapter 1. We agreed that we have a Mind which resides in a Body that uses Language and exists in an external World.
The mind is a Consciousness that has Desires, Emotions, and Memories.
It is contained in a physical Body that can Act, Sense, and Create.
We use language comprising Signs, with Definitions, Images, and Concepts.
All this takes place in an external world made of Things experiencing Forces and having Properties, all of which are Connected.
All of this was represented in the diagram;
The mind is a Consciousness that has Desires, Emotions, and Memories.
It is contained in a physical Body that can Act, Sense, and Create.
We use language comprising Signs, with Definitions, Images, and Concepts.
All this takes place in an external world made of Things experiencing Forces and having Properties, all of which are Connected.
All of this was represented in the diagram;
As we consider these and other examples of our experience we will recognize a fractal like symmetry in virtually everything we encounter or experience. Large or small, connected or disparate, the patterns are the same. Eventually we will be able to develop a simple and easy to use familiarity with this fractal symmetry of the universe. With practice this will become almost instinctive, literally integrated into our very being. When this happens things will get more fun, more productive and satisfying. You will start to look at things from a new perspective.
Chapter 3
The Relational Science Model
Science creates models based on observation and evidence to predict and understand a perceived physical reality. Science forms hypotheses, tests them through observation and experimentation, and then accepts them, rejects them, or reformulates them for further analysis and testing. Belief is established via the evidence that this process provides.
The collection of models that comprises modern science describes phenomena that occur in certain specified areas of application. The models have precise definitions for what they consider and the areas or boundaries that specify where and how the models can be usefully applied. Some of these models are enormously powerful and have generated technologies that we all use regularly.
Currently there are two main types of scientific models. The first type are the natural sciences which comprise general models for physics, chemistry, and biology. Natural science also includes the derivative applied sciences of engineering, medicine, agriculture, and electronics and computers. All of these models assume that the universe exists as a physical reality that is independent from any connection to consciousness or conscious entities.
The second type of scientific model deals with the social sciences whose subjects include areas of study like economics, psychology, and sociology. These models are applied to conscious entities, specifically people, that use language and exist in a physical universe. However, the fundamental principles of these models are not viewed as being an essential component of the universe as a whole. Instead, they are considered as applying only to a part of the universe, and that they may possibly be derived from the natural sciences in the future.
The natural sciences differ from the social sciences primarily in terms of methodology and area of application. Natural science uses scientific procedures based on the formation of hypotheses for which there is supporting evidence. Such hypotheses may be testable with reproducible experimentation, or they may be supported through observations that can be validated by others. These procedures are applied to a universe that is viewed as existing independently from consciousness or conscious entities. It is believed by some that natural science can eventually explain consciousness through the use of its scientific methodologies.
The social sciences in contrast deal primarily with phenomena that are involved with conscious entities and the activities of conscious entities. The universe of natural science, and the scientific methodologies which the natural sciences use, are included wherever they may be relevant or useful. However, other perceptions of the universe and other methods of inquiry are also used if and where they also help make confirmable or useful predictions.
Despite the successes of all the models from both the natural and the social sciences, they do not explain all of our experience. For example they can describe, but cannot explain, the fundamental nature of our consciousness and the consequent impact that this has on our own behavior and emotions.
The Relational Science Model proposes to unify the natural and social sciences, and also establish a relational symmetry with religion. The critically essential and most daunting and challenging aspect of this task is to satisfactorily explain how the inclusion of consciousness and language can still explain all of the experimentally validated achievements of the natural sciences in a new paradigm. Consequently, that is where we begin.
Natural science had its formal origins in the atomistic hypothesis of Leucippus and Democritus in the mid fifth century BC. This proposed that all matter is composed of tiny particles, called atoms. These particles exist in a space described by Pythagoras and later Euclid, as a geometry comprising length, width, and height, or distance, area, and volume or solid.
Over the next two thousand years these ideas evolved, eventually coalescing in the 16th and 17th centuries into a more detailed model based on the work of Galileo, Kepler, Newton, Leibniz, Descartes, and others. This model comprised a formal scientific method, a mathematical calculus, and a Cartesian coordinate system that allowed for the combination of Euclidean geometry and algebra. Motion was described as to how the location of matter within the coordinates of a Cartesian Coordinate System changed with time. Matter was still perceived as being comprised of atoms or particles.
Additional features emerged in the 18th and 19th centuries concerning the structure and organization of the chemical elements, Maxwell’s electromagnetic theory, and the existence of the electron, and radioactivity. These discoveries merged with the
Newtonian framework of motion comprising forces acting on masses within a Euclidean geometry as described by a Cartesian coordinate system. By the beginning of the 20th century this had set the stage for a model of atomic structure that comprised a positively charged core with orbiting negatively charged electrons.
Also during the 18th and 19th centuries the various models of living biological phenomena such as botany, zoology, bacteriology, genetics, evolution, and biochemistry were starting to get connected to physics and chemistry. By the early 20th century this had resulted in a sort of comprehensive model of the natural sciences that was based on atomically organized matter existing in a universe describable with time and a three dimensional Cartesian coordinate system. This Classical Science model is still useful today and provides for a working understanding of how things actually work in our everyday experience.
However, this situation changed in the rest of the 20th century with the development of General Relativity and Quantum Mechanics. These two models dramatically altered the way that natural science looked at the universe. The fundamental assumptions, that space could be adequately described with a Cartesian coordinate system, and that atoms and the known subatomic particles were inviolate, they could not be created or destroyed, were changed. Although the new assumptions, and the models that derived from them, were extremely difficult to understand, the models that emerged from them proved to be much more powerful than the various models that comprised the Classical Science. Most of the earlier models were explained and often extended by the two new models which quickly subsumed the earlier work.
But problems remained. Despite the successes of General Relativity and Quantum Mechanics these two models remain philosophically incompatible, and neither of them can resolve the issues of consciousness and language. The Relational Paradigm Science Model is proposed as a way of resolving these problems. To understand how this can occur, it is necessary to look at the foundational presumptions that underly the two dominant models of modern physics, General Relativity and Quantum Mechanics.
In General Relativity Einstein rejected the notion that the motion of objects that had mass could be adequately explained in terms of a universal frame of reference in which the changes of three spatial coordinates of a Cartesian Coordinate system could be measured with respect to changes in time. He argued that the description of such motion had to be independent of the choice of the frame of reference and would be valid only if it was consistently transformable from one frame of reference to another independent of the choice of coordinate system.
The geometry of Euclid in which relationships (eg. measurements made with rulers and clocks) are made relative to fixed straight lines (sequences of real numbers) was thus replaced with a differential geometry in which relationships are described relative to each other and not to some fixed external standard. Thus motion was viewed as a path or geodesic in the geometry and this has been viewed as seeing space as “curved” and not linear. Since energy is classically defined in terms of the motion of mass, going to a differential geometry resulted in an equivalence principle between inertial and gravitational mass and the representation of mass as energy.
Thus mass became a property of the space-time geometry. From the relational perspective this is symmetrical to viewing consciousness as a property of the relational structure of the universe. Mass as a property of geometry and consciousness as a property of language are equivalent relational symmetries.
The description of differential geometry led to the use of tensors as a means of describing the relative changes of each variable in a space with respect to other variables in that space, and how that can be compared with descriptions in other spaces. (Spaces being defined in terms of the number of independent variables required to describe phenomena with respect to who is doing the description.)
Using General Relativity certain predictions were made that were not consistent with Classical Science but which were nonetheless verified by observation and experiment. But General Relativity did not deal with electric charge and how charges are combined in atoms. It also did not explain the observations that atoms could be interacted in ways that showed that they are comprised of additional component parts, the sub atomic particles.
To explain these phenomena Quantum Mechanics was developed by Bohr, Schrodinger, Heisenberg, Pauli, Dirac, and others, and this has developed into our most successful theory. Called the Standard Model it describes the chemical, electrical, and radioactive phenomena that occur on an atomic and subatomic scale. This description explains an extensive amount of everyday phenomena and leads to our current technologies in electronics (such as cell phones and computers) and the chemical, material, and nuclear sciences.
The Standard Model presents a more complex view of the atom than the one that comprised the photon, electron, proton, and neutron of the Classical Science. In the Standard Model the atoms are still viewed as containing electrons and photons, but these are now seen as being members of groups of additional subatomic particles such as quarks, leptons, and bosons. The nuclei of atoms also contains positively charged protons and neutrons but these are themselves composed of quarks. Negatively charged electrons are now viewed as surrounding the nuclei in orbitals which have to be described in terms of probabilities and complex numbers.
Different numbers of electrons can occupy the orbitals but have to do so in a manner that was consistent with a property called spin. Thus an electron is viewed as rotating and its spin is described in terms of its “intrinsic angular momentum” which could be right handed or left handed. This determines the number and types of electrons that can be in any given orbital.
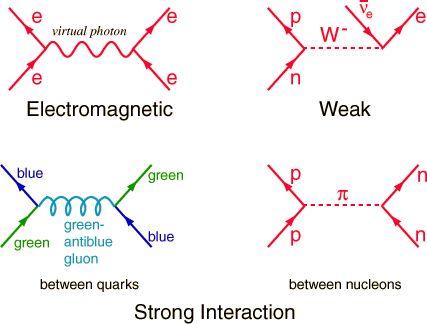
The subatomic particles are classified as either matter particles, the quarks and leptons, or transfer particles, the bosons. The transfer particles only exist when mediating the interactions of the matter particles via one of three fundamental forces or interactions, the electromagnetic, weak nuclear, and strong nuclear interaction.
This view of Quantum Mechanics did not include the fourth fundamental interaction in physics which was the gravitational interaction that is described in General Relativity. As of now this still has not been successfully integrated into the Quantum Mechanical Standard Model.
The General Relativity description of space-time is not required in the Standard Model which in general works successfully with the Euclidean Cartesian Coordinate geometry of the Classical Science, or its modification as described in special relativity where time as a fourth dimension is defined as time multiplied by the speed of light.
We know that to be credible the Relational Symmetries must show that the incorporation of consciousness and language into the foundations of science has to be consistent with all the experiential successes of physics, and that specifically means that this has to include the successes of both General Relativity and Quantum Mechanics.
To show how the Relational Science Model can apply to both General Relativity and Quantum Mechanics, (as well as provide a basis for the inclusion of the social sciences and religion), it is important to recognize that the relational symmetries occur in the foundations of our number systems and in many areas of mathematics. In particular, it is essential to know that the notion of relational symmetry is manifested in the quaternion, a type of complex number that is crucial in modern physics. A description of this background is presented in Appendix A.
General Relativity assumes that the universe is continuous and deterministic, and that matter is perceived as local configurations of a continuous field. Quantum Mechanics views the universe as discrete and probabilistic, and that matter is perceived in terms of individual particles that are separate from each other. The perceived incompatibilities of these two models arises because they are each defined on different parts of the universe. Neither of them consider the universe as a whole because they do not include consciousness and language.
The Relational Symmetry Paradigm explains this incompatibility because both primary Relational Symmetries are linguistic reflections of each other as perceived by conscious entities. Consequently, they both are compatible and consistent elements in an explanation of the basic structure and functioning of the whole universe. In the...
... symmetry the ● specifies a unique point or perspective of a continuous infinite universe. But in the...
... symmetry the point as a creative consciousness exists as...
... a self relational distinction that establishes a boundary between itself and the rest of the universe. This creates the perspective of a particle with a boundary...
... separating a point ● from the rest of the universe. This in turn generates the concept of a boundary for the universe itself, that is relative to every point consciousness in the universe. Such a concept creates the idea of a unique location in the universe for each conscious entity. It also can be described in terms of the concept of particles within the universe as comprising boundaries separating locations and processes in space and time from the rest of the universe.
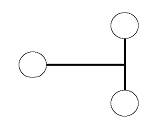
These particles can be visualized as;
These particles can be visualized as;
Which could also be represented as;
or
Each of these diagrams shows a different interpretation of how the self relational nature of both the point ● and the boundary...
... can be used in the Relational Symmetry diagrams. It also illustrates why we have the idea that there are several fundamentally different conceptions of particles in the universe. This is symmetrical to how we earlier looked at our own organizations from both a structural and procedural perspective.
These ideas are reflected in how Quantum Mechanics now proposes that there are three fundamental types of particles. The first of these are the fundamental and non divisible particles themselves; the up and down quarks, the electron, and (possibly) the neutrinos. The second type of particles are those that are composed of stable combinations of the first type. These only exist because of a third type of particle, the transfer particles which are called bosons. These particles are only detectable for very short periods of time in situations where other particles are interacting with each other in very high energy situations or in radioactive decay.
A new way of looking at this considers that the...
These ideas are reflected in how Quantum Mechanics now proposes that there are three fundamental types of particles. The first of these are the fundamental and non divisible particles themselves; the up and down quarks, the electron, and (possibly) the neutrinos. The second type of particles are those that are composed of stable combinations of the first type. These only exist because of a third type of particle, the transfer particles which are called bosons. These particles are only detectable for very short periods of time in situations where other particles are interacting with each other in very high energy situations or in radioactive decay.
A new way of looking at this considers that the...
... formalism is symmetrical with the mathematical quaternion that is used extensively in quantum mechanics, and which can also be compatibly combined with the tensor formulation of general relativity. A potential unification of the Quantum Mechanics and General Relativity models can then be achieved by casting space-time itself as a Relational Symmetry quaternion in which particles are perceived in terms of the...
Relational Symmetry that is a reflection of the...
...quaternion space time geometry. This is described in more detail in Appendix B.
It is interesting to note that the mathematical equations used to describe both General Relativity and Quantum Mechanics are generally agnostic with respect to time. They often work as well for negative values of time as they do for positive values of time. We all know that this is not the case for our personal experience which only deals with positive time and that results in our experiences being non reversible.
Part of this difficulty stems from the inability of physics to provide a physical meaning to the concept of i, the square root of minus one. Thus applications of complex numbers and quaternions are often structured in terms of complex conjugates so that the solutions of equations can be obtained from the real parts and the complex parts can be ignored. (This is the rational for the use of Hilbert spaces in Quantum Mechanics.) From the Relational perspective i is viewed as a mathematical function of the concept of memory. Consciousness exists in the present. The future is a representation of linguistic predictions and the past exists as memories. By equating i as a function of memory its presence in the quaternion equations becomes understandable and provides an additional tool for application.
To fully understand how time is incorporated into the Relational Science Model we add entropy, and in particular, the Maximum Entropy Principle, to the interpretations of the universe. We also assume that thermodynamic entropy is equivalent to informational entropy.
The basis for this assumption has evolved from the historical evolution of the concept of entropy. In physics the 2nd Law of Thermodynamics is essentially a statement about entropy. This can be experimentally measured thermodynamically and can be defined in statistical mechanics and quantum mechanics in terms of
energy distributions, microstates, and probabilities. However, entropy only exists in chemical reactions that occur in positive time. In fact, it was the necessity to define an entropy term for each chemical reaction to account for the observations that chemical reactions cannot be reversed without adding additional energy. There are no perpetual motion machines in nature. Time as we experience it is positive. Memories are negative time.
The key concept in understanding entropy and time is that of probabilities and how they have evolved to include consciousness and language. To illustrate how this occurred consider its historical development.
In 1713 a work by James (Jacques) Bernoulli presented the first formal definition of probability which he called the "Principle of Insufficient Reason". This stated that given a situation containing a number of possible cases, none of whom we know to be more or less likely than any other, then the probability of an event dependent on some of these cases would be the total number of cases favorable to this event divided by the total number of possible cases.
Bernoulli also extended this understanding to situations which could be well described but in which not all of the possible cases would be equally likely. He did this by relating probability to experimentally observed frequencies. Thus in his famous theorem he showed that over a large number of repetitions an observed ratio of events will not differ from its probability by more than an arbitrarily small amount. This was the first time that a formal principle had been presented for specific applications of the concepts of probability, and that marked the beginning of probability theory as a branch of mathematics.
Probability theory began to approach the problem of inference with the work of Thomas Bayes (1763). His results made it possible to estimate the probability of one event given knowledge of the probability of a related event.
All of this work was then collected and extended by Laplace (1749 - 1827) into an extensive treatment of mathematical probability theory. He expanded the work of Bernoulli and Bayes into a generalized procedure. This made it possible to estimate future probabilities of causally related events given the occurrence of certain initial events and the a priori probabilities of these initial events. The only problem with applying this result (known as Bayes' theorem) is that, unless Bernoulli's Principle
of Insufficient Reason holds and all the a priori probabilities are equal, there is no way to estimate the a priori probabilities.
After Laplace probability theory itself stagnated while its applications continued to grow. Part of this can be attributed to a significant change in the understanding of the nature of probability. Instead of a ratio of favored over possible it began to be viewed as a frequency function. Thus a probability was determined relative to a given experiment and was defined as a limiting value of a very large number of repetitions of this experiment.
This view gradually began to change and then a series of critical discoveries were made.
The first of these was published in 1946 by Richard T. Cox. He showed that the basic mathematical nature of probabilities was independent of any reality other than the existence of language. Cox demonstrated that for a given linguistically stated hypothesis and a carefully defined set of inferences based on that hypothesis, a unique mathematical function could be defined which was identical to probability as used in the basic equations of probability theory. This meant that probability theory itself was derivable solely from language and a requirement that the theory be internally consistent. It did not have to rely on experiment or a relation to observable frequency functions in an external world.
At about the same time a paper by Claude Shannon in 1948 extended the concept of entropy, which had previously been primarily associated with thermodynamics, into information theory. He showed that for a given probability distribution there exists a function which is a unique and unambiguous measure of the amount of uncertainty associated with that probability distribution. Since this function had the same mathematical expression as the formula used in statistical mechanics for entropy, it was called the entropy of the probability distribution.
Then in 1957 Edwin T. Jaynes published the Maximum Entropy Principle (MEP). He used Shannon's entropy function, in conjunction with Cox's proof as to the linguistic nature of probability, to propose a general principle of plausible inference. This states that given certain information the best choice of a probability distribution based on that information will be the one which maximizes its entropy.
While Jaynes derived the maximum entropy principle primarily for statistical mechanics he did recognize that it was indeed a general principle of inference.
Thus it will hold regardless of what type of situation is to be described by the probability distribution. Because it provided a "best" way to pick a priori probabilities it therefore solved the major problem which had hindered application of Bayes fundamental theorem as recognized and stated by Laplace. Consequently the maximum entropy principle became a model for rational decision making.
Because it was considered to be a truly generalized method of logical inference it was assumed that it was equally valid in both physics and information theory. Thus it was viewed as a way to make a “best” decision based on the available information that can be represented in terms of inferences based on one or more hypotheses. This can be viewed as a way of considering the available information so that each piece of evidence is balanced with respect to all the other pieces of evidence so that they collectively optimize their impact on the basic entropy function. Note that if there is no relevant evidence available then the entropy function will treat all possible inferences equally.
Shortly after Jaynes published the maximum entropy principle L. Bianchi and J.R. Hamann realized that it was of foundational importance in the origin and definition of life itself. They claimed that in order to build a consistent theory of living systems it was necessary to include the maximum entropy principle in the foundations of a hierarchical system of organization stemming from a series of personal presumptions.
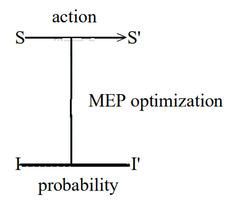
The Relational Symmetry Paradigm proposes that understanding the structure of the MEP can be useful in situations where it is not possible to formally define a system in terms of inferences based on hypotheses. Consider a state variable X that represents a Relational Symmetry, for example...
It is interesting to note that the mathematical equations used to describe both General Relativity and Quantum Mechanics are generally agnostic with respect to time. They often work as well for negative values of time as they do for positive values of time. We all know that this is not the case for our personal experience which only deals with positive time and that results in our experiences being non reversible.
Part of this difficulty stems from the inability of physics to provide a physical meaning to the concept of i, the square root of minus one. Thus applications of complex numbers and quaternions are often structured in terms of complex conjugates so that the solutions of equations can be obtained from the real parts and the complex parts can be ignored. (This is the rational for the use of Hilbert spaces in Quantum Mechanics.) From the Relational perspective i is viewed as a mathematical function of the concept of memory. Consciousness exists in the present. The future is a representation of linguistic predictions and the past exists as memories. By equating i as a function of memory its presence in the quaternion equations becomes understandable and provides an additional tool for application.
To fully understand how time is incorporated into the Relational Science Model we add entropy, and in particular, the Maximum Entropy Principle, to the interpretations of the universe. We also assume that thermodynamic entropy is equivalent to informational entropy.
The basis for this assumption has evolved from the historical evolution of the concept of entropy. In physics the 2nd Law of Thermodynamics is essentially a statement about entropy. This can be experimentally measured thermodynamically and can be defined in statistical mechanics and quantum mechanics in terms of
energy distributions, microstates, and probabilities. However, entropy only exists in chemical reactions that occur in positive time. In fact, it was the necessity to define an entropy term for each chemical reaction to account for the observations that chemical reactions cannot be reversed without adding additional energy. There are no perpetual motion machines in nature. Time as we experience it is positive. Memories are negative time.
The key concept in understanding entropy and time is that of probabilities and how they have evolved to include consciousness and language. To illustrate how this occurred consider its historical development.
In 1713 a work by James (Jacques) Bernoulli presented the first formal definition of probability which he called the "Principle of Insufficient Reason". This stated that given a situation containing a number of possible cases, none of whom we know to be more or less likely than any other, then the probability of an event dependent on some of these cases would be the total number of cases favorable to this event divided by the total number of possible cases.
Bernoulli also extended this understanding to situations which could be well described but in which not all of the possible cases would be equally likely. He did this by relating probability to experimentally observed frequencies. Thus in his famous theorem he showed that over a large number of repetitions an observed ratio of events will not differ from its probability by more than an arbitrarily small amount. This was the first time that a formal principle had been presented for specific applications of the concepts of probability, and that marked the beginning of probability theory as a branch of mathematics.
Probability theory began to approach the problem of inference with the work of Thomas Bayes (1763). His results made it possible to estimate the probability of one event given knowledge of the probability of a related event.
All of this work was then collected and extended by Laplace (1749 - 1827) into an extensive treatment of mathematical probability theory. He expanded the work of Bernoulli and Bayes into a generalized procedure. This made it possible to estimate future probabilities of causally related events given the occurrence of certain initial events and the a priori probabilities of these initial events. The only problem with applying this result (known as Bayes' theorem) is that, unless Bernoulli's Principle
of Insufficient Reason holds and all the a priori probabilities are equal, there is no way to estimate the a priori probabilities.
After Laplace probability theory itself stagnated while its applications continued to grow. Part of this can be attributed to a significant change in the understanding of the nature of probability. Instead of a ratio of favored over possible it began to be viewed as a frequency function. Thus a probability was determined relative to a given experiment and was defined as a limiting value of a very large number of repetitions of this experiment.
This view gradually began to change and then a series of critical discoveries were made.
The first of these was published in 1946 by Richard T. Cox. He showed that the basic mathematical nature of probabilities was independent of any reality other than the existence of language. Cox demonstrated that for a given linguistically stated hypothesis and a carefully defined set of inferences based on that hypothesis, a unique mathematical function could be defined which was identical to probability as used in the basic equations of probability theory. This meant that probability theory itself was derivable solely from language and a requirement that the theory be internally consistent. It did not have to rely on experiment or a relation to observable frequency functions in an external world.
At about the same time a paper by Claude Shannon in 1948 extended the concept of entropy, which had previously been primarily associated with thermodynamics, into information theory. He showed that for a given probability distribution there exists a function which is a unique and unambiguous measure of the amount of uncertainty associated with that probability distribution. Since this function had the same mathematical expression as the formula used in statistical mechanics for entropy, it was called the entropy of the probability distribution.
Then in 1957 Edwin T. Jaynes published the Maximum Entropy Principle (MEP). He used Shannon's entropy function, in conjunction with Cox's proof as to the linguistic nature of probability, to propose a general principle of plausible inference. This states that given certain information the best choice of a probability distribution based on that information will be the one which maximizes its entropy.
While Jaynes derived the maximum entropy principle primarily for statistical mechanics he did recognize that it was indeed a general principle of inference.
Thus it will hold regardless of what type of situation is to be described by the probability distribution. Because it provided a "best" way to pick a priori probabilities it therefore solved the major problem which had hindered application of Bayes fundamental theorem as recognized and stated by Laplace. Consequently the maximum entropy principle became a model for rational decision making.
Because it was considered to be a truly generalized method of logical inference it was assumed that it was equally valid in both physics and information theory. Thus it was viewed as a way to make a “best” decision based on the available information that can be represented in terms of inferences based on one or more hypotheses. This can be viewed as a way of considering the available information so that each piece of evidence is balanced with respect to all the other pieces of evidence so that they collectively optimize their impact on the basic entropy function. Note that if there is no relevant evidence available then the entropy function will treat all possible inferences equally.
Shortly after Jaynes published the maximum entropy principle L. Bianchi and J.R. Hamann realized that it was of foundational importance in the origin and definition of life itself. They claimed that in order to build a consistent theory of living systems it was necessary to include the maximum entropy principle in the foundations of a hierarchical system of organization stemming from a series of personal presumptions.
The Relational Symmetry Paradigm proposes that understanding the structure of the MEP can be useful in situations where it is not possible to formally define a system in terms of inferences based on hypotheses. Consider a state variable X that represents a Relational Symmetry, for example...
The probabilities that any given sign in this symbolic formalism will be relationally symmetrical with the other three signs cannot be calculated in the way that the MEP can be numerically calculated because we do not have a precise understanding of the signs of the Relational Symmetries in terms of inferences and hypotheses. However, the Maximum Entropy solution can be sensed as a process by a living conscious organism in a manner that is comparable to how entropy exists in any given chemical reaction.
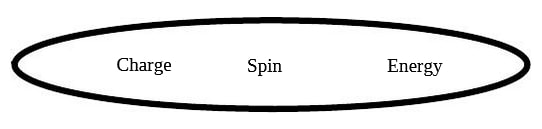
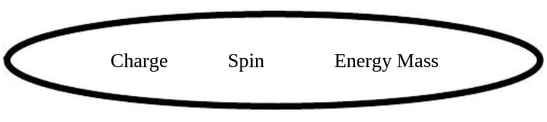
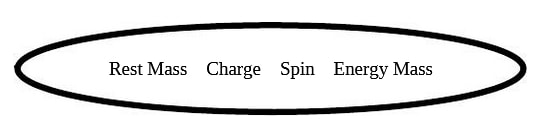
This provides an understanding of how the nature of particles (seen as boundaries) in a quaternion space time can also comprise charge, spin, and mass. The particles were recognized as forms of the original Relational Symmetries that were expanded by considering the boundary nature of self relation. This was visualized as;
This provides an understanding of how the nature of particles (seen as boundaries) in a quaternion space time can also comprise charge, spin, and mass. The particles were recognized as forms of the original Relational Symmetries that were expanded by considering the boundary nature of self relation. This was visualized as;
Which could also be represented...
or...
In each of those diagrams of the various particles, the original symbolic elements can be combined in different Maximum Entropy configurations that represent how a particle or a consciousness can exist within and of the universe. This symmetry applies regardless of whether the MEP can be numerically calculated and it combines both the structure and the process aspects of our reality. This is described in more detail in Appendix C.
We as conscious entities frequently encounter situations where a calculation of the MEP is not possible or practical. This occurs throughout biology where we do not fully understand the linguistic or semiotic nature of any given living system. Despite not knowing these details we still believe that it is valid to apply this symmetrical extension of the MEP to the way that all living systems are structured and make decisions. Any action taken by a living system is the result of a decision made in terms of a language or semiotic system used by the living system. Consequently the physical entropy changes of the resulting action are compatible with, and representable by the MEP used to make the decision, as long as the information available for that decision is a valid representation of the situation.
What this means is that each individual organism makes decisions that lead to actions that obey the MEP and consequently obey the physical Laws of Thermodynamics. This is true even if we cannot calculate this due to the complexity of the organism and situation, or our unfamiliarity with the language of the organism itself.
The “languages" that comprise our normal experience include a cellular semiotic code of DNA, RNA, and protein synthesis, a neurological cybernetic language involving dendrites and neurotransmitters or computer programing languages, and natural languages used by humans, and some higher vertebrates and invertebrates. This results in three trophic layers of biological organization, all of which involve the MEP as to how the individual organisms act, how the populations of organisms act within a given layer, and how the multitrophic layers themselves interact with each other. As you can see the complexity is enormous and each action we, or any other living organism, takes is almost always indeterminate from a computational perspective.
Fortunately, nature does not do the math in the same way that we do the math. The entropy is just an integral part of the geometry of the universe and all actions and motions are consistent with some sort of linguistic representation associated with the conscious entity that initiated the action or motion. There are no numerical calculations that the physical world does to cause this.
An interpretation of what this might mean involves the concept of quantum entanglement in physics. This proposes that objects that have been interacted with each other and then separated could still share some condition or state. Einstein famously opposed this idea and called it “spooky action at a distance”. Despite his objections there is experimental evidence that seems to support such entanglement.
The Relational Science Model would suggest that this mystifying phenomena may be understandable in terms of the language used to frame the hypotheses and define the experimental apparatus used to verify it. Evidence supporting this view has recently emerged from work that provides an explanation of quantum entanglement in terms of the maximum entropy principle (MEP).
Finally, adding some understanding and formal representation of entropy and the Maximum Entropy Principle makes it possible to fully integrate biology,
psychology, and sociology with physics and chemistry. The key issue is that although nature does not do math the way that we do the math, the way conscious entities make decisions is still compatible with the MEP. The formal expression of the MEP is just an incomplete and simplistic representation of an aesthetic and artistic process that is the essence of the Relational Symmetry Paradigm and is the actual manifestation of the relational symmetries in our lives.
To Summarize:
The Relational Symmetry Paradigm is a tool that has been developed from history, our own personal experiences, and mathematics and science to help us understand how to live a peaceful cooperative existence with each other and the planet. To use this tool we have to;
Covariantly communicate with each other.
Honestly disclose what we really believe.
Not tell lies.
If we fail to do this, in science or politics, we may end up living on an increasingly unrecognizable and dangerous planet, or dying in a world that no longer supports life as we know it.
We as conscious entities frequently encounter situations where a calculation of the MEP is not possible or practical. This occurs throughout biology where we do not fully understand the linguistic or semiotic nature of any given living system. Despite not knowing these details we still believe that it is valid to apply this symmetrical extension of the MEP to the way that all living systems are structured and make decisions. Any action taken by a living system is the result of a decision made in terms of a language or semiotic system used by the living system. Consequently the physical entropy changes of the resulting action are compatible with, and representable by the MEP used to make the decision, as long as the information available for that decision is a valid representation of the situation.
What this means is that each individual organism makes decisions that lead to actions that obey the MEP and consequently obey the physical Laws of Thermodynamics. This is true even if we cannot calculate this due to the complexity of the organism and situation, or our unfamiliarity with the language of the organism itself.
The “languages" that comprise our normal experience include a cellular semiotic code of DNA, RNA, and protein synthesis, a neurological cybernetic language involving dendrites and neurotransmitters or computer programing languages, and natural languages used by humans, and some higher vertebrates and invertebrates. This results in three trophic layers of biological organization, all of which involve the MEP as to how the individual organisms act, how the populations of organisms act within a given layer, and how the multitrophic layers themselves interact with each other. As you can see the complexity is enormous and each action we, or any other living organism, takes is almost always indeterminate from a computational perspective.
Fortunately, nature does not do the math in the same way that we do the math. The entropy is just an integral part of the geometry of the universe and all actions and motions are consistent with some sort of linguistic representation associated with the conscious entity that initiated the action or motion. There are no numerical calculations that the physical world does to cause this.
An interpretation of what this might mean involves the concept of quantum entanglement in physics. This proposes that objects that have been interacted with each other and then separated could still share some condition or state. Einstein famously opposed this idea and called it “spooky action at a distance”. Despite his objections there is experimental evidence that seems to support such entanglement.
The Relational Science Model would suggest that this mystifying phenomena may be understandable in terms of the language used to frame the hypotheses and define the experimental apparatus used to verify it. Evidence supporting this view has recently emerged from work that provides an explanation of quantum entanglement in terms of the maximum entropy principle (MEP).
Finally, adding some understanding and formal representation of entropy and the Maximum Entropy Principle makes it possible to fully integrate biology,
psychology, and sociology with physics and chemistry. The key issue is that although nature does not do math the way that we do the math, the way conscious entities make decisions is still compatible with the MEP. The formal expression of the MEP is just an incomplete and simplistic representation of an aesthetic and artistic process that is the essence of the Relational Symmetry Paradigm and is the actual manifestation of the relational symmetries in our lives.
To Summarize:
The Relational Symmetry Paradigm is a tool that has been developed from history, our own personal experiences, and mathematics and science to help us understand how to live a peaceful cooperative existence with each other and the planet. To use this tool we have to;
Covariantly communicate with each other.
Honestly disclose what we really believe.
Not tell lies.
If we fail to do this, in science or politics, we may end up living on an increasingly unrecognizable and dangerous planet, or dying in a world that no longer supports life as we know it.
Appendix A
Numbers and Mathematics
To show how the Relational Symmetry Paradigm can unify General Relativity and Quantum Mechanics, as well as provide a basis for the inclusion of the social sciences and religion, it is useful, and perhaps necessary, to start with an examination of how the relational symmetries occur in our number systems and how these are used in certain areas of mathematics. In particular, it will be essential to see how the notion of the first Relational Symmetry is manifested in the quaternion, a type of complex number that is crucial in modern physics.
Mathematics first started with a sense of shape and counting. These were relationally expressed as both geometry, which maps into the Relational Symmetries as;
To show how the Relational Symmetry Paradigm can unify General Relativity and Quantum Mechanics, as well as provide a basis for the inclusion of the social sciences and religion, it is useful, and perhaps necessary, to start with an examination of how the relational symmetries occur in our number systems and how these are used in certain areas of mathematics. In particular, it will be essential to see how the notion of the first Relational Symmetry is manifested in the quaternion, a type of complex number that is crucial in modern physics.
Mathematics first started with a sense of shape and counting. These were relationally expressed as both geometry, which maps into the Relational Symmetries as;
and number, which comprises; four types of numbers, the natural, rational, real, and complex numbers. These map into the Relational Symmetry as;
The introduction of the boundary relation allowed us to combine the geometric and numerical interpretations as;
Again remember that this is only one of the representations of how the relational symmetries can combine with each other and that this does not represent the full range of how numbers and geometrical forms can be combined. In particular, it does not imply that lines in the sense of ┃ are comprised of points even though we often consider them to be.
The symbols that are commonly used in how we represent and use numbers also show a relational symmetry;
The symbols that are commonly used in how we represent and use numbers also show a relational symmetry;
It is important here to note that these concepts exist in our minds as linguistic constructs in our memories. If science wants to presume that it will only deal with an independent physical reality that is not related in any way to consciousness and language then these constructs do not exist in that reality. They are useful in the models we create to explain such an independent physical reality but that does not mean that they exist in that reality.
Similarly, how numbers are related to each other also comprises additional symmetries. This can be seen in basic mathematics, which again shows a relational symmetry.
Similarly, how numbers are related to each other also comprises additional symmetries. This can be seen in basic mathematics, which again shows a relational symmetry.
This symmetry is used in algebra or group theory.
Each type of number (called a number field) has its own type of algebra with a defining operation which embodies the essence of the conceptual basis for the number field;
Each type of number (called a number field) has its own type of algebra with a defining operation which embodies the essence of the conceptual basis for the number field;
The shape geometrical concept reappears when the second Relational Symmetry is applied starting with the concept of boundary. This can lead to a generation of set theory as a foundational way to derive the various number fields.
Before beginning a discussion as to how the Relational Symmetries are compatible with set theory it is important to note that numbers and mathematics are a part of language and do not represent a perceived physical reality in the sense that the descriptions and calculations of science do. This perception of the universe changes when consciousness and language are included in the domain of science.
The relevance here becomes apparent when we consider the foundations of set theory. This is important since set theory can be used to generate the algebras and groups that describe each of the four fundamental number fields. The application of the set theory derivation of numbers to the physical realities of distance, surface, volume, and space have made it extraordinarily useful in science. Thus it has emerged as a general foundation for all of mathematics. Set theory was originally formulated by Cantor in 1874 in conjunction with the work of Dedekind on real numbers to describe how infinities could be included in mathematics.
A set was defined as a mathematical object, sort of like the concept of a number, but generalized to comprise a boundary that would contain all of the numbers of a certain field. For example, sets could be defined to contain all of the counting numbers, the positive integers, or all of the rational numbers, the fractions. Thus a set containing all the real numbers would include all the integers, the fractions, the exponentials, the logarithms, and the transcendental numbers that had been
discovered throughout history, This set then included an infinite number of infinite groups of numbers.
Despite this, set theory proved to be very useful. Thus the concept of set was generalized as a boundary that could include any collection of real or imagined entities, including other sets, apples, or numbers, or whatever. These were defined as elements or members of the set. A subset could then be defined to contain each element of the set. To complete this general language based definition of set theory certain properties of sets were defined and these included the operations of union and intersection.
The problem with all this is that it generated certain paradoxes and antinomies. The most famous of these was the Russell antinomy of “The set of all sets that are not members of themselves, is it a member of itself?”. Many of these problems were resolved by generating axiomatic formulations of set theory, and set theory is today viewed as the foundations of virtually all of mathematics. However, some problems remain as exemplified by the Godel incompleteness theorems, the persistence of infinities, and questions about boundaries that require descriptions of classes or collections before sets can be rigorously defined.
To resolve these issues it is useful to recognize and identify common linguistic tendencies that can lead to problems when incorporated in the presentation of numbers and mathematics. For example;
A simple question that we would normally answer with a yes or no, can be compromised with an “I don’t know” or an “I forgot”. Binary choices which are derived exclusively from a linear relation often do not convey these aspects of what we are or should be saying. To resolve this look at such situations from the perspective of the relations comprising the relational symmetry. The ┃ sign is the binary choice, yes or no, true or false.
From the ┣ sign perspective “I don’t know” or “maybe” becomes a possibility that should always be considered when asked to respond to a question with a binary, ┃, yes or no answer. This is particularly relevant with respect any discussion of probabilities.
A similar situation concerns statements that are considered to be true or false. Take the statement that says “This statement is false.” If it is true, it is false, and if it is false, it is true. Such statements again need to be understood or considered from
the ┣ relational sign perspective as possibly being meaningless, uncertain, ambiguous, irrelevant, or unnecessary. Again, it is important to consider the ┣ relation before committing to the binary, ┃, true or false response.
Because the Relational Paradigm Science Model has included consciousness and language as part of the universe to be described by science the existence of these types of linguistic statements creates a problem when science uses mathematics in its descriptions of the universe. Most pure mathematical systems rely on a propositional logic for an axiomatic presentation of their definitions, and this requires that statements about the definitions either be, demonstrably true or false, or presumptions that are assumed to be true or false.
Such restrictions lead to concepts and statements that have uncertain or indeterminant meaning, or even worse, they themselves may be meaningless. These include; infinity, infinitesimal, nothing, everything, and anything. Such concepts may serve a purpose for pure mathematics as an abstract self contained discipline, but they are not necessary for a mathematics that is pragmatically useful in applications. The inclusion of these types of concepts tends to produce statements that are paradoxes or antimonies. To resolve this situation consider the following replacements;
Infinity. sufficiently large
Infinitesimal sufficiently small
Nothing not a known thing
Everything every known thing
Anything any known thing
To explain, consider a series of things where each next member of the series is larger than the preceding member, the counting numbers for example. This series is often considered to be infinite in that it has no known end. For any positive integer that you can define there is always a larger one that can be generated by adding one to the number you just defined. Hence the concept of infinity seems to have meaning. Replace this with the concept of sufficiently large which occurs when you can’t pragmatically distinguish one large thing or number from the next large thing or number in the series.
You also can replace the concept of nothing with no known thing, where known connotes the existence of evidence for the thing in question. Similarly, for everything and anything.
From this perspective it is important to make a preliminary presumption that a statement that defines a boundary that only contains itself is a meaningless statement. It is like the statement “This statement is false”. This embodies the concept of cancellation and can be symbolically formalized with the diagram;
The relevance here becomes apparent when we consider the foundations of set theory. This is important since set theory can be used to generate the algebras and groups that describe each of the four fundamental number fields. The application of the set theory derivation of numbers to the physical realities of distance, surface, volume, and space have made it extraordinarily useful in science. Thus it has emerged as a general foundation for all of mathematics. Set theory was originally formulated by Cantor in 1874 in conjunction with the work of Dedekind on real numbers to describe how infinities could be included in mathematics.
A set was defined as a mathematical object, sort of like the concept of a number, but generalized to comprise a boundary that would contain all of the numbers of a certain field. For example, sets could be defined to contain all of the counting numbers, the positive integers, or all of the rational numbers, the fractions. Thus a set containing all the real numbers would include all the integers, the fractions, the exponentials, the logarithms, and the transcendental numbers that had been
discovered throughout history, This set then included an infinite number of infinite groups of numbers.
Despite this, set theory proved to be very useful. Thus the concept of set was generalized as a boundary that could include any collection of real or imagined entities, including other sets, apples, or numbers, or whatever. These were defined as elements or members of the set. A subset could then be defined to contain each element of the set. To complete this general language based definition of set theory certain properties of sets were defined and these included the operations of union and intersection.
The problem with all this is that it generated certain paradoxes and antinomies. The most famous of these was the Russell antinomy of “The set of all sets that are not members of themselves, is it a member of itself?”. Many of these problems were resolved by generating axiomatic formulations of set theory, and set theory is today viewed as the foundations of virtually all of mathematics. However, some problems remain as exemplified by the Godel incompleteness theorems, the persistence of infinities, and questions about boundaries that require descriptions of classes or collections before sets can be rigorously defined.
To resolve these issues it is useful to recognize and identify common linguistic tendencies that can lead to problems when incorporated in the presentation of numbers and mathematics. For example;
A simple question that we would normally answer with a yes or no, can be compromised with an “I don’t know” or an “I forgot”. Binary choices which are derived exclusively from a linear relation often do not convey these aspects of what we are or should be saying. To resolve this look at such situations from the perspective of the relations comprising the relational symmetry. The ┃ sign is the binary choice, yes or no, true or false.
From the ┣ sign perspective “I don’t know” or “maybe” becomes a possibility that should always be considered when asked to respond to a question with a binary, ┃, yes or no answer. This is particularly relevant with respect any discussion of probabilities.
A similar situation concerns statements that are considered to be true or false. Take the statement that says “This statement is false.” If it is true, it is false, and if it is false, it is true. Such statements again need to be understood or considered from
the ┣ relational sign perspective as possibly being meaningless, uncertain, ambiguous, irrelevant, or unnecessary. Again, it is important to consider the ┣ relation before committing to the binary, ┃, true or false response.
Because the Relational Paradigm Science Model has included consciousness and language as part of the universe to be described by science the existence of these types of linguistic statements creates a problem when science uses mathematics in its descriptions of the universe. Most pure mathematical systems rely on a propositional logic for an axiomatic presentation of their definitions, and this requires that statements about the definitions either be, demonstrably true or false, or presumptions that are assumed to be true or false.
Such restrictions lead to concepts and statements that have uncertain or indeterminant meaning, or even worse, they themselves may be meaningless. These include; infinity, infinitesimal, nothing, everything, and anything. Such concepts may serve a purpose for pure mathematics as an abstract self contained discipline, but they are not necessary for a mathematics that is pragmatically useful in applications. The inclusion of these types of concepts tends to produce statements that are paradoxes or antimonies. To resolve this situation consider the following replacements;
Infinity. sufficiently large
Infinitesimal sufficiently small
Nothing not a known thing
Everything every known thing
Anything any known thing
To explain, consider a series of things where each next member of the series is larger than the preceding member, the counting numbers for example. This series is often considered to be infinite in that it has no known end. For any positive integer that you can define there is always a larger one that can be generated by adding one to the number you just defined. Hence the concept of infinity seems to have meaning. Replace this with the concept of sufficiently large which occurs when you can’t pragmatically distinguish one large thing or number from the next large thing or number in the series.
You also can replace the concept of nothing with no known thing, where known connotes the existence of evidence for the thing in question. Similarly, for everything and anything.
From this perspective it is important to make a preliminary presumption that a statement that defines a boundary that only contains itself is a meaningless statement. It is like the statement “This statement is false”. This embodies the concept of cancellation and can be symbolically formalized with the diagram;
This diagram was initially formulated by George Spencer Brown in his “Laws of Form”. The importance of this concept is that this “law of cancelation”, resolves the Russell antimony of “The set of all sets that are not members of themselves, is it a member of itself?”. This is meaningless. A set that contains itself doesn’t exist.
This brings the Parmenidean question of “Does nothing exist?” into context with the concept of boundary. In particular, can there be a boundary between everything and nothing. Consider the two diagrams;
This brings the Parmenidean question of “Does nothing exist?” into context with the concept of boundary. In particular, can there be a boundary between everything and nothing. Consider the two diagrams;
and
Are these diagrams equivalent? Can there even be a set that contains nothing? Isn’t that equivalent to saying that the universe is bounded and that there is nothing
outside of the universe. To avoid all these problems we assume that all these statements are indeterminant at best, and, at worst, meaningless in the sense of “This statement is False”.
So, with all this in mind, construct a non axiomatic description of set theory as follows. Define a set, X, as a boundary containing elements. An element can be anything, real or imagined. The elements of X are other boundaries, each of which also contains one or more elements. The boundary of X is not an element of X. Each boundary in X is defined as a subset of X. On X are defined two binary operations, union and intersection. The Union of a subset, A, and a subset, B, defines a subset, C, of X that contains all of the elements that are in A and B. The intersection of subset, A, and subset, B, defines a subset, D, of X that contains only those elements that are in both A and B. The set X also contains a subset Y that contains all elements that are in any of the subsets of X. The set Y is called the universal subset of X. The set X also contains a subset N that does not contain any element that is already contained in any subset of X. This subset is called the empty subset of X.
...relation.
By combing these relations with the...
By combing these relations with the...
...relation we can make comparisons and the results of these comparisons can be labelled with the...
...relation. Call these , equivalence relations and they include the concepts of equal, not equal, more than, less than, similar to, not similar to, and other comparable concepts. Combining all these relations via the...
...relation allows for the creation of functions and operations in set theory. Thus for a Set X as previously described, the self relational symmetries are
An accurate description of this can be visualized through the use of Venn diagrams which were developed by John Venn in 1880 as a way to represent the set theoretic ideas the Cantor had proposed in 1874. Shown below, each set is represented as a circle. The union of the two sets comprises both circles. The intersection of the two sets comprises only the middle area that exists in each circle.
The set inclusions can also can be visualized as;
Which could also be represented as;
or
These definitions can in turn be used to generate the rings, integral domains, and fields of mathematics which define the four fundamental types or fields of numbers discussed earlier.
These symbolic formalisms exhibit symmetry with other symbolic formalisms that employ graphical representations that have previously been proposed by others. These include the existential graphs of Charles Sander Peirce. It is significant that Peirce also cast doubt on the use of infinities when describing geometrical entities in terms of boundary, ie numerical, concepts. He saw this as conflicting with the understanding of lines, planes, or solids as continuous things. Hence representing them in terms of real numbers would reach a situation where the separation of two points that were arbitrarily close, that is, were indistinguishable in that their separation was sufficiently small, would merge them together. Either point would be adequate to describe a location in the line or plane or volume but this description would not be a point in the line or plane or volume itself.
It is relevant to note that Peirce’s theory of signs and his focus on “Firstness”, “Secondness”, and “Thirdness” was a precursor to the one – three fourness structure of the Relational Symmetries. This initially emerged in Hamann’s Relational Systems formalism and has now evolved into the Relational Symmetries and their combination into the Relational Symmetry Paradigm.
Other graphical or symbolic formalisms that are symmetric with the Relational Symmetries can be found in the Boundary Mathematics of William Bricken. He also saw that there were major problems with the axiomatic approaches and the embrace of concepts that included the contradictions and paradoxes that arise from the linear thinking of propositional logics.
Other examples include the diagrams from the “Laws of Form” of George Spence Brown as previously mentioned, and the symbolic diagrams of Bliss Symbols or those used in the visual basic programming language.
Now consider the quaternion. This is a mathematical object originally introduced by William Rowan Hamilton in 1843 and later assimilated by William Kingdom Clifford in 1878 – 1882 as one of the Clifford algebras.
A quaternion is a number with a form of;
a1 + bv + cj + dk
Where a, b, c, and d are real numbers and 1 is the unitary concept of one, and v, j, and k are non equivalent imaginary numbers each equal to the square root of minus one. Let * represent multiplication, then
v * v = - 1, j * j = - 1, k * k = - 1
and v * j = - k, j * k = - v, k * v = - j
but i, j, and k are not equal to each other.
A better visualization of this can be obtained from a matrix representation of the quaternion basis elements;
These symbolic formalisms exhibit symmetry with other symbolic formalisms that employ graphical representations that have previously been proposed by others. These include the existential graphs of Charles Sander Peirce. It is significant that Peirce also cast doubt on the use of infinities when describing geometrical entities in terms of boundary, ie numerical, concepts. He saw this as conflicting with the understanding of lines, planes, or solids as continuous things. Hence representing them in terms of real numbers would reach a situation where the separation of two points that were arbitrarily close, that is, were indistinguishable in that their separation was sufficiently small, would merge them together. Either point would be adequate to describe a location in the line or plane or volume but this description would not be a point in the line or plane or volume itself.
It is relevant to note that Peirce’s theory of signs and his focus on “Firstness”, “Secondness”, and “Thirdness” was a precursor to the one – three fourness structure of the Relational Symmetries. This initially emerged in Hamann’s Relational Systems formalism and has now evolved into the Relational Symmetries and their combination into the Relational Symmetry Paradigm.
Other graphical or symbolic formalisms that are symmetric with the Relational Symmetries can be found in the Boundary Mathematics of William Bricken. He also saw that there were major problems with the axiomatic approaches and the embrace of concepts that included the contradictions and paradoxes that arise from the linear thinking of propositional logics.
Other examples include the diagrams from the “Laws of Form” of George Spence Brown as previously mentioned, and the symbolic diagrams of Bliss Symbols or those used in the visual basic programming language.
Now consider the quaternion. This is a mathematical object originally introduced by William Rowan Hamilton in 1843 and later assimilated by William Kingdom Clifford in 1878 – 1882 as one of the Clifford algebras.
A quaternion is a number with a form of;
a1 + bv + cj + dk
Where a, b, c, and d are real numbers and 1 is the unitary concept of one, and v, j, and k are non equivalent imaginary numbers each equal to the square root of minus one. Let * represent multiplication, then
v * v = - 1, j * j = - 1, k * k = - 1
and v * j = - k, j * k = - v, k * v = - j
but i, j, and k are not equal to each other.
A better visualization of this can be obtained from a matrix representation of the quaternion basis elements;
Using standard matrix multiplication shows;
The quaternion matrix representation discloses an interesting view of how the primary symbolic formalism itself impacts our understanding of the quaternion. The following argument shows how the symbolic formalism of the primary Relational Symmetry actually is isomorphic to a quaternion. Let
● 1 a point, an origin
┃ v one vertical line
┣ j one sidebar line and one right vertical line
H k one left vertical line, one sidebar line, and one right vertical line
Define a binary operation * which combines any two primary symbols in a left-right linear fashion such that if they exactly superimpose they cancel back to a point but with a change of sign, and if they cross to form the third of the three primary symbols, but never completely superimpose on them, this also results in a change of sign. The ● acts as a unity. Thus
● * ● = ●
● * ┃ = ┃
● * ┣ = ┣
● * H = H
- ● * ● = - ●
- ● * ┃ = - ┃
- ● * ┣ = - ┣
- ● * H = - H
- ● * - ● = ●
┃ * ┃ = - ●
┣ * ┣ = - ●
H * H = - ●
┃ * ┣ = - H The ┃crosses the ┣ which creates a sign change and then combines with it to yield a - H , no cancellation.
┣ * H = - ┃ The ┣ combines with the H . Then the ┣ combines with the left vertical and cross bar of the H , cancelling them all and creating a sign change. This leaves a - ┃
H * ┃ = -┣ The H combines with the ┃ and this results in the ┃ combining with the right vertical of the H such that they both cancel and this creates a sign change, leaving a - ┣
This shows that a quaternion is isomorphically symmetrical to the symbolic formalism of the first Relational Symmetry. It is also important to note that if the ┣ sign is changed to ┫ the Relational Symmetry still behaves as a quaternion, only the last three equations have a positive result. Thus the primary Relational Symmetry itself can have a left or right handed orientation and this duality will emerge relative to positive and negative charge and male and female organisms.
● 1 a point, an origin
┃ v one vertical line
┣ j one sidebar line and one right vertical line
H k one left vertical line, one sidebar line, and one right vertical line
Define a binary operation * which combines any two primary symbols in a left-right linear fashion such that if they exactly superimpose they cancel back to a point but with a change of sign, and if they cross to form the third of the three primary symbols, but never completely superimpose on them, this also results in a change of sign. The ● acts as a unity. Thus
● * ● = ●
● * ┃ = ┃
● * ┣ = ┣
● * H = H
- ● * ● = - ●
- ● * ┃ = - ┃
- ● * ┣ = - ┣
- ● * H = - H
- ● * - ● = ●
┃ * ┃ = - ●
┣ * ┣ = - ●
H * H = - ●
┃ * ┣ = - H The ┃crosses the ┣ which creates a sign change and then combines with it to yield a - H , no cancellation.
┣ * H = - ┃ The ┣ combines with the H . Then the ┣ combines with the left vertical and cross bar of the H , cancelling them all and creating a sign change. This leaves a - ┃
H * ┃ = -┣ The H combines with the ┃ and this results in the ┃ combining with the right vertical of the H such that they both cancel and this creates a sign change, leaving a - ┣
This shows that a quaternion is isomorphically symmetrical to the symbolic formalism of the first Relational Symmetry. It is also important to note that if the ┣ sign is changed to ┫ the Relational Symmetry still behaves as a quaternion, only the last three equations have a positive result. Thus the primary Relational Symmetry itself can have a left or right handed orientation and this duality will emerge relative to positive and negative charge and male and female organisms.
Appendix B
A Proposed Unification of Quantum Mechanics and General Relativity
A Proposed Unification of Quantum Mechanics and General Relativity
To show how the Relational Science Model can apply to modern physics we begin by showing that the...
formalism is symmetrical with the mathematical quaternion that is used extensively in quantum mechanics. It is also compatible with the tensor formulation of general relativity. The unification of the Quantum Mechanics and General Relativity models might then be achieved by casting space-time itself as a Relational Symmetry quaternion.
The development of this hypothesis starts with the work of Mendel Sachs who took a suggestion made by Einstein, but never followed up by him, to include quaternions in General Relativity. Sachs work is described in detail in two books; “General Relativity and Matter; A Spinor Field Theory from Fermis to Light-Years”, and “Quantum Mechanics from General Relativity; An Approximation for a Theory of Inertia” (4).
This approach kept the Riemann curvature tensor formulation as the differential geometry of space-time but combined it with the algebra of the quaternion spinor formulation instead of the algebra of the real number field. Since the real number algebra is commutative under multiplication, whereas the quaternion algebra is non commutative for three of the quaternion basis elements, use of the quaternion algebra expanded the metric tensor from ten independent variables to sixteen independent variables. This allowed Sachs to include many quantum mechanical interactions in his formulation of General Relativity. However, this still did not explain all of the interactions of the Standard Model of Quantum Mechanics.
The Relational Symmetries approach suggests that this could be taken one step further by assuming that the geometry of space-time is itself a quaternion. Actually the assumption is that the space-time geometry of the universe is symmetrically relational, as foundationally described by the archetypal relational diagrams, and that this can be mathematically applied to space-time through the quaternion representation.
Note: I actually had the opportunity to discuss this application with Mendel Sachs. He felt that using a quaternion geometry instead of a quaternion algebra should not change the conclusions of his work. Either approach should be valid. The modification of the algebra of the tensor representation should not change how the quaternion impacts the calculations.
One of the immediate consequences of this is that all equations of motion become wave equations. In Quantum Mechanics a wave function can be linked to the square of a complex number. This was introduced in 1926 by Max Born as a probability amplitude which served as an interpretation of the values of a wave function. Since any equation of motion in a four dimensional quaternion geometry must, by definition, be expressed by complex numbers, probability amplitudes are a natural interpretation of any measurement of motion.
It is also possible that the interpretation of space time as a quaternion may provide a path to explain the apparent existence of antimatter and the dark matter and dark energy that the current models do not explain. Unfortunately, a discussion of these possibilities is beyond the scope of this work.
Using the quaternion representation for the space-time geometry does not appreciably alter Sachs presentation for General Relativity. However, it does have an impact on how we view the Standard Model of Quantum Mechanics. Examination of the Standard Model Lagrangian shows that spinor and quaternion representations are used extensively to describe the quantum behavior of the subatomic interactions of the Standard Model.
This is shown through the inclusion of the Pauli matrices which provided the mathematics needed for the Pauli exclusion principle that determines how electrons exist in atomic orbitals, and the Dirac equation that integrates quantum mechanics with the special theory of relativity . The Pauli matrices are;
The development of this hypothesis starts with the work of Mendel Sachs who took a suggestion made by Einstein, but never followed up by him, to include quaternions in General Relativity. Sachs work is described in detail in two books; “General Relativity and Matter; A Spinor Field Theory from Fermis to Light-Years”, and “Quantum Mechanics from General Relativity; An Approximation for a Theory of Inertia” (4).
This approach kept the Riemann curvature tensor formulation as the differential geometry of space-time but combined it with the algebra of the quaternion spinor formulation instead of the algebra of the real number field. Since the real number algebra is commutative under multiplication, whereas the quaternion algebra is non commutative for three of the quaternion basis elements, use of the quaternion algebra expanded the metric tensor from ten independent variables to sixteen independent variables. This allowed Sachs to include many quantum mechanical interactions in his formulation of General Relativity. However, this still did not explain all of the interactions of the Standard Model of Quantum Mechanics.
The Relational Symmetries approach suggests that this could be taken one step further by assuming that the geometry of space-time is itself a quaternion. Actually the assumption is that the space-time geometry of the universe is symmetrically relational, as foundationally described by the archetypal relational diagrams, and that this can be mathematically applied to space-time through the quaternion representation.
Note: I actually had the opportunity to discuss this application with Mendel Sachs. He felt that using a quaternion geometry instead of a quaternion algebra should not change the conclusions of his work. Either approach should be valid. The modification of the algebra of the tensor representation should not change how the quaternion impacts the calculations.
One of the immediate consequences of this is that all equations of motion become wave equations. In Quantum Mechanics a wave function can be linked to the square of a complex number. This was introduced in 1926 by Max Born as a probability amplitude which served as an interpretation of the values of a wave function. Since any equation of motion in a four dimensional quaternion geometry must, by definition, be expressed by complex numbers, probability amplitudes are a natural interpretation of any measurement of motion.
It is also possible that the interpretation of space time as a quaternion may provide a path to explain the apparent existence of antimatter and the dark matter and dark energy that the current models do not explain. Unfortunately, a discussion of these possibilities is beyond the scope of this work.
Using the quaternion representation for the space-time geometry does not appreciably alter Sachs presentation for General Relativity. However, it does have an impact on how we view the Standard Model of Quantum Mechanics. Examination of the Standard Model Lagrangian shows that spinor and quaternion representations are used extensively to describe the quantum behavior of the subatomic interactions of the Standard Model.
This is shown through the inclusion of the Pauli matrices which provided the mathematics needed for the Pauli exclusion principle that determines how electrons exist in atomic orbitals, and the Dirac equation that integrates quantum mechanics with the special theory of relativity . The Pauli matrices are;
Multiplying these by i , the square root of minus one, generates the three non unitary basis elements of the quaternion.
By using the quaternion geometry the inclusion of the quaternion and spinor representations in the Standard Model Lagrangian can be viewed as leading to a view that spin and charge, as well as mass, are integral parts of the relational geometric nature of the universe, as manifested in the particle concept.
If...
By using the quaternion geometry the inclusion of the quaternion and spinor representations in the Standard Model Lagrangian can be viewed as leading to a view that spin and charge, as well as mass, are integral parts of the relational geometric nature of the universe, as manifested in the particle concept.
If...
...represents the quaternion space time then attach the following representations of...
as...
Particles can be shown in a variety of configurations as;
or
or
In the Relational Science Model the geometry for both General Relativity and Quantum Mechanics is represented as a quaternion geometry. Mass is represented as occurring in two forms, a rest mass which is manifested in quarks and leptons, and a relativistic (energy) mass as manifested in photons and gluons. In the Standard Model both photons and gluons are shown as having no particle mass but they both are “energy packets” that exchange energy between and among other stable particles which do have a particle mass. The W, Z, and Higgs bosons also act as exchange particles even though they have particle masses.
The basic stable particles are the electron, the up quark, and the down quark, all of which are charged; and the electron neutrino, the muon neutrino, and the tau neutrino, all of which are uncharged. The other particles are high energy combinations that are unstable.
A way of visualizing the Standard Model and the interactions that occur in Quantum Physics comprises the Feynman diagrams. These diagrams were developed in 1948 by Richard Feynman and promoted extensively by Freeman Dyson. An example of these diagrams that illustrates a way of visualizing the electromagnetic, weak nuclear and strong nuclear interactions is;
The basic stable particles are the electron, the up quark, and the down quark, all of which are charged; and the electron neutrino, the muon neutrino, and the tau neutrino, all of which are uncharged. The other particles are high energy combinations that are unstable.
A way of visualizing the Standard Model and the interactions that occur in Quantum Physics comprises the Feynman diagrams. These diagrams were developed in 1948 by Richard Feynman and promoted extensively by Freeman Dyson. An example of these diagrams that illustrates a way of visualizing the electromagnetic, weak nuclear and strong nuclear interactions is;
This diagram is from the Hyperphysics website (5).
The Feynman diagrams are basically symmetrical with the Relational Symmetries but they use the Minkowski extension of the Cartesian coordinate system that was developed for special relativity. Consider the possibility that these diagrams are related to events that occur in a General Relativity quaternion space-time geometry and that the diagrams themselves may be depictions of “energy packets” that also include charge and spin. Thus the diagrams of interactions that appear to involve multiple particles relate to concepts of expanded energy packets whose boundaries end once the interaction is completed with the appearance of stable particles.
The Feynman diagrams are not precise descriptions of an external physical reality but are instead symbolic formalisms that act as a guide as to how to perform mathematical calculations that can successfully predict observed results that occur in high energy physics experiments. Thus they serve to help us understand what the processes might be that underlie Quantum Mechanics. This is similar to the way that the Relational Symmetry Paradigm proposes to assist us in understanding both ourselves and the universe within which we live and function. The assumption is that the true nature of the universe may be beyond what we can completely describe with our existing languages but that we can effectively approximate an understanding of this universe that is useful in how we live our lives through the simple symbolic formalisms of the Relational Symmetries.
The Feynman diagrams are basically symmetrical with the Relational Symmetries but they use the Minkowski extension of the Cartesian coordinate system that was developed for special relativity. Consider the possibility that these diagrams are related to events that occur in a General Relativity quaternion space-time geometry and that the diagrams themselves may be depictions of “energy packets” that also include charge and spin. Thus the diagrams of interactions that appear to involve multiple particles relate to concepts of expanded energy packets whose boundaries end once the interaction is completed with the appearance of stable particles.
The Feynman diagrams are not precise descriptions of an external physical reality but are instead symbolic formalisms that act as a guide as to how to perform mathematical calculations that can successfully predict observed results that occur in high energy physics experiments. Thus they serve to help us understand what the processes might be that underlie Quantum Mechanics. This is similar to the way that the Relational Symmetry Paradigm proposes to assist us in understanding both ourselves and the universe within which we live and function. The assumption is that the true nature of the universe may be beyond what we can completely describe with our existing languages but that we can effectively approximate an understanding of this universe that is useful in how we live our lives through the simple symbolic formalisms of the Relational Symmetries.
Appendix C
An Expanded Maximum Entropy Concept
Classically the Maximum Entropy Principle (MEP) is a generalized method of logical inference which is defined on a system in terms of inferences based on hypotheses.
The procedure is to pick a system that can be described in terms of a state variable, call it X, which can take on a series of numerical values. Thus X represents a hypothesis that the state variable exists, that it can be exhaustively described in terms of a fixed number of inferences, and that these inferences can be associated with specific numerical values. Assign a probability to each of these possible values, p(j), such that p(j) descries the probability that the jth value will occur. This then becomes a number associated with the linguistic statement that the jth inference will occur given the linguistic hypothesis presented by the state variable X.
(For example, consider a die, a cube with six faces and a number from one through six on each face with no repetitions. The p(j) represent the probabilities that when the die is thrown, the jth face will be on top.)
If there is no additional information then the entropy S of the general situation is represented by;
S = - Σj p(j) ln p(j)
Where there are n possible inferences based on the hypothesis of X.
Usually this term is constrained by the condition that the sum of all n probabilities must equal one.
If there is additional information available such that one or more expected value functions, F(u,j), can be defined on X then these provide additional constraints for a calculation of the best probability distribution for p(j). Here u is an index for the number of such expected value functions that are available such that;
< Fu > = ∑j p(j)F(u,j)
Can be summed over all possible values of j, and < Fu > is the expected value for the F(u,j) function.
Given m available expected value functions the MEP can be calculated using the method of Lagrange multipliers to determine the “best” probability distribution for p(j), where best is usually interpreted in terms of maximizing our uncertainty for any situation or decision. The basic equation is;
S = [-p(j) ln p(j) + λ*(p(j) - 1) + Σu( λu p(j)F(u,j) - < Fu >)]
Where S is the constrained entropy, λ represents a Lagrange multiplier, and there are n different p(j) probabilities and m different <Fu> expected value functions. Setting S equal to zero and differentiating with respect to p(j) gives;
-1 – ln p(j) + λ* + (Σu λu F(u,j)
Setting λ0 = λ* -1 gives
P(j) = e exp λ0 + e exp (Σu λu F(u,j)
An alternative way to view this situation is to use numerical techniques to iteratively select values for p(j) and λu such that S will be a maximum.
One of the first applications of the relational systems theory of Jon Ray Hamann was a generalized decision model. In this model a system, S, is going to act and thereby achieve a new state, S'. The system S contains I, information about past and present conditions, and I', projections of possible futures. These are related to each other by value judgements and/or assignments of probabilities. These evaluations or probabilities are in turn related to the action changing S into S' by a decision or optimization procedure
The procedure is to pick a system that can be described in terms of a state variable, call it X, which can take on a series of numerical values. Thus X represents a hypothesis that the state variable exists, that it can be exhaustively described in terms of a fixed number of inferences, and that these inferences can be associated with specific numerical values. Assign a probability to each of these possible values, p(j), such that p(j) descries the probability that the jth value will occur. This then becomes a number associated with the linguistic statement that the jth inference will occur given the linguistic hypothesis presented by the state variable X.
(For example, consider a die, a cube with six faces and a number from one through six on each face with no repetitions. The p(j) represent the probabilities that when the die is thrown, the jth face will be on top.)
If there is no additional information then the entropy S of the general situation is represented by;
S = - Σj p(j) ln p(j)
Where there are n possible inferences based on the hypothesis of X.
Usually this term is constrained by the condition that the sum of all n probabilities must equal one.
If there is additional information available such that one or more expected value functions, F(u,j), can be defined on X then these provide additional constraints for a calculation of the best probability distribution for p(j). Here u is an index for the number of such expected value functions that are available such that;
< Fu > = ∑j p(j)F(u,j)
Can be summed over all possible values of j, and < Fu > is the expected value for the F(u,j) function.
Given m available expected value functions the MEP can be calculated using the method of Lagrange multipliers to determine the “best” probability distribution for p(j), where best is usually interpreted in terms of maximizing our uncertainty for any situation or decision. The basic equation is;
S = [-p(j) ln p(j) + λ*(p(j) - 1) + Σu( λu p(j)F(u,j) - < Fu >)]
Where S is the constrained entropy, λ represents a Lagrange multiplier, and there are n different p(j) probabilities and m different <Fu> expected value functions. Setting S equal to zero and differentiating with respect to p(j) gives;
-1 – ln p(j) + λ* + (Σu λu F(u,j)
Setting λ0 = λ* -1 gives
P(j) = e exp λ0 + e exp (Σu λu F(u,j)
An alternative way to view this situation is to use numerical techniques to iteratively select values for p(j) and λu such that S will be a maximum.
One of the first applications of the relational systems theory of Jon Ray Hamann was a generalized decision model. In this model a system, S, is going to act and thereby achieve a new state, S'. The system S contains I, information about past and present conditions, and I', projections of possible futures. These are related to each other by value judgements and/or assignments of probabilities. These evaluations or probabilities are in turn related to the action changing S into S' by a decision or optimization procedure
In this discussion I represents some state variable X which is expressed in terms of a probability distribution p(j) and various quantifiable functions. I' represents the expected value functions determined by projections made relative to available information. The MEP then determines the “best” or least biased decision based on this information. It should be noted that the calculation of p(j) can become very difficult for even moderately complex situations and this limits the area of applicability for the MEP.
The Relational Symmetry Paradigm proposes that understanding the structure of the MEP can be useful in situations where it is not possible to formally define a system in terms of inferences based on hypotheses. Consider a description of a state variable X that represents a Relational Symmetry, for example...
The Relational Symmetry Paradigm proposes that understanding the structure of the MEP can be useful in situations where it is not possible to formally define a system in terms of inferences based on hypotheses. Consider a description of a state variable X that represents a Relational Symmetry, for example...
Let the ● relation represent the entropy term, and the other three relational forms represent three expected value functions. Thus
|
Then require that
|
Σj [p(j)] = 1
|
If we could define functions for the
┃,┣ , H relations that are expressible with numbers we could solve this equation by choosing values for λ1, λ2, λ3, and the p(j) such that the sum of the four constraints is a maximum. This would balance our Maximum Entropy equation. The p(j) would then be the probability that any given sign in this symbolic formalism will be relationally symmetrical with the other three signs.
However, when we cannot define functions for the relational terms that are representable with numbers we can still make balance (aesthetic or artistic) judgements about our description. These would not be calculated in the way that the MEP can be calculated given precise inferences based on a hypothesis, because we do not have a precise understanding of the signs of the Relational Symmetries
in terms of inferences and hypotheses. However, the Maximum Entropy solution can be sensed by a living conscious organism in a manner that is comparable to how entropy exists in any given chemical reaction. Note that this formulation of the MEP constrained by three expected value functions is symmetrical with the one three fourness of the quaternion. This suggests that there are additional ways that conscious entities understand and evaluate information in creative and decision making processes.
Nature does not use numbers to calculate a chemical reaction entropy. However, we consider it, and calculate it if we can, whenever we examine a real world chemical event. But whether we can do the calculation or not, the reaction occurs and the entropy change of the reaction also occurs. Since we are composed of chemical elements undergoing chemical reactions all the time we have a connection to, and sense of, the entropy component of the reactions. If we have an awareness of this connection we can sense when it is in balance. This is commonly called intuition. That is what the Relational Symmetry Paradigm is all about. It allows us to make a “best” decision or judgement based on who we are and what we know.
This is similar to the guidance that the Feynman diagrams confer to physicists doing Quantum Mechanical calculations. The diagrams do not directly reflect a physical reality but they are useful in helping us make calculations and predictions as to how to how that reality might behave in certain situations. The Relational Symmetry Paradigm serves a comparable function for us when we try to understand ourselves and the universe in the situations where the known paradigms of science, religion, and politics break down.
┃,┣ , H relations that are expressible with numbers we could solve this equation by choosing values for λ1, λ2, λ3, and the p(j) such that the sum of the four constraints is a maximum. This would balance our Maximum Entropy equation. The p(j) would then be the probability that any given sign in this symbolic formalism will be relationally symmetrical with the other three signs.
However, when we cannot define functions for the relational terms that are representable with numbers we can still make balance (aesthetic or artistic) judgements about our description. These would not be calculated in the way that the MEP can be calculated given precise inferences based on a hypothesis, because we do not have a precise understanding of the signs of the Relational Symmetries
in terms of inferences and hypotheses. However, the Maximum Entropy solution can be sensed by a living conscious organism in a manner that is comparable to how entropy exists in any given chemical reaction. Note that this formulation of the MEP constrained by three expected value functions is symmetrical with the one three fourness of the quaternion. This suggests that there are additional ways that conscious entities understand and evaluate information in creative and decision making processes.
Nature does not use numbers to calculate a chemical reaction entropy. However, we consider it, and calculate it if we can, whenever we examine a real world chemical event. But whether we can do the calculation or not, the reaction occurs and the entropy change of the reaction also occurs. Since we are composed of chemical elements undergoing chemical reactions all the time we have a connection to, and sense of, the entropy component of the reactions. If we have an awareness of this connection we can sense when it is in balance. This is commonly called intuition. That is what the Relational Symmetry Paradigm is all about. It allows us to make a “best” decision or judgement based on who we are and what we know.
This is similar to the guidance that the Feynman diagrams confer to physicists doing Quantum Mechanical calculations. The diagrams do not directly reflect a physical reality but they are useful in helping us make calculations and predictions as to how to how that reality might behave in certain situations. The Relational Symmetry Paradigm serves a comparable function for us when we try to understand ourselves and the universe in the situations where the known paradigms of science, religion, and politics break down.
Notes and References
Notes:
1. A new type of thinking is essential if mankind is to survive and move toward higher levels.
From "Atomic Education Urged by Einstein", New York Times (25 May 1946), and later quoted in the article "The Real Problem is in the Hearts of Man" by Michael Amrine, from the New York Times Magazine (23 June 1946). A slightly modified version of the 23 June article was reprinted in Einstein on Peace by Otto Nathan and Heinz Norden (1960), and it was also reprinted in Einstein on Politics by David E. Rowe and Robert Schulmann (2007), p. 383.
From "Atomic Education Urged by Einstein", New York Times (25 May 1946), and later quoted in the article "The Real Problem is in the Hearts of Man" by Michael Amrine, from the New York Times Magazine (23 June 1946). A slightly modified version of the 23 June article was reprinted in Einstein on Peace by Otto Nathan and Heinz Norden (1960), and it was also reprinted in Einstein on Politics by David E. Rowe and Robert Schulmann (2007), p. 383.
2. Quote by Richard Buckminster Fuller: “If you want to teach people a new way of thinking...” (goodreads.com)
3. Relational Systems Theory
Personal Communication with Jon Ray Hamann
4. “General Relativity and Matter; A Spinor Field Theory from Fermis to Light-Years”, Mendel Sachs, D. Reidel Publishing Company, 1982, and “Quantum Mechanics from General Relativity; An Approximation for a Theory of Inertia”, Mendel Sachs, D. Reidel Publishing Company, 1986
5. Diagram is from the Hyperphysics website link, see Exchange Particles (gsu.edu) Which is copyright protected and used herein for non commercial purposes. See HyperPhysics Concepts (gsu.edu) This is an excellent site for the presentation of basic concepts in physics
3. Relational Systems Theory
Personal Communication with Jon Ray Hamann
4. “General Relativity and Matter; A Spinor Field Theory from Fermis to Light-Years”, Mendel Sachs, D. Reidel Publishing Company, 1982, and “Quantum Mechanics from General Relativity; An Approximation for a Theory of Inertia”, Mendel Sachs, D. Reidel Publishing Company, 1986
5. Diagram is from the Hyperphysics website link, see Exchange Particles (gsu.edu) Which is copyright protected and used herein for non commercial purposes. See HyperPhysics Concepts (gsu.edu) This is an excellent site for the presentation of basic concepts in physics
References:
Bayes, Thomas, Phil. Trans. Roy. Soc., p, 330, (1763).
Bernoulli, Jacques, (1713), ARS CONJECTANDI.
Bianchi, Luigi, M. and Hamann, Jon, R., J. Theor. Biol., 28, p. 489, (1970).
Cox, Richard T., Am. J. Phys. 17, p. 1, (1946) and THE ALGEBRA OF PROBABLE INFERENCE, Johns Hopkins University Press (1961).
Descartes, Rene, (1637), DISCOURSE ON THE METHOD, p. 7, as reprinted by Thomas Nelson and Sons, New York (1954).
Descartes, Rene, (1641), MEDITATIONS ON FIRST PHILOSOPHY as reprinted by Thomas Nelson and Sons, New York (1954).
Einstein, Albert, (1916), The Foundation of the General Theory of Relativity, Annalen der Physik, 49, translated by W. Perrett and G. B. Jeffery in 1923, and published in THE PRINCIPLE OF RELATIVITY, Dover Publications, New York.
Goedel, Kurt, "On Formally Undecidable Propositions of Principia Mathematica and Related Systems", (1931).
Hamann, Jon Ray, MultiCoRelationalism see MultiCoRelationism (MCR): 2019
Heisenburg, Werner, THE PHYSICAL PRINCIPLES OF THE QUANTUM THEORY, translated by C. Eckart and C. Holt, University of Chicago Press, Chicago, (1930), Dover Publications, New York, (1949).
Jaynes, Edwin T., Phys. Rev., 106, p. 620; 108, p. 171, (1957). See also Jaynes and others in; Levine, R. D. and Tribus, M., editors, THE MAXIMUM ENTROPY FORMALISM, The MIT Press, (1979).
Laplace, Pierre Simon, Marquis de, THEORIE ANALYTIQUE DES PROBABILITIES, 3rd edition, (1820).
Leibniz, Gottfried Wilhelm, MONADOLOGY, (1714) in LEIBNIZ PHILOSOPHICLA WRITINGS, edited by G. H. R. Parkinson, translated by Mary Morris and G. H. R. Parkinson, J. M. Dent & Sons: London, (1973).
Peirce, Charles Sanders, see COLLECTED PAPERS OF CHARLES SANDERS PEIRCE, volumes 1 - 6 edited by C. Hartshorne and P. Weiss, (1931-1935). In particular see the Pragmatism Lectures at Harvard (1903) in vol. 5, pp. 14 - 212, and the articles on "What Pragmatism is" from The Monist (1905) in vol. 5 pp. 411 - 463. Perice’s thinking on discrete points in a continuum is presented in REASONING AND THE LOGIC OF THINGS, edited by Kenneth Laine Ketner, pg 159-160. This section is from the reprint of the third of his 1898 Harvard Lectures, “The Logic of Relatives”
Russell, Bertrand, "On Some Difficulties in the Theory of Transfinite Numbers and Order Types", Proc. London Math. Soc., ser. 2, 4, p.29, (1906).
Shannon, Claude, Bell System Tech. J., 27, p. 379, 623, (1948), reprinted in THE MATHEMATICAL THEORY OF COMMUNICATION, University of Illinois Press, Urbana (1949).
Bayes, Thomas, Phil. Trans. Roy. Soc., p, 330, (1763).
Bernoulli, Jacques, (1713), ARS CONJECTANDI.
Bianchi, Luigi, M. and Hamann, Jon, R., J. Theor. Biol., 28, p. 489, (1970).
Cox, Richard T., Am. J. Phys. 17, p. 1, (1946) and THE ALGEBRA OF PROBABLE INFERENCE, Johns Hopkins University Press (1961).
Descartes, Rene, (1637), DISCOURSE ON THE METHOD, p. 7, as reprinted by Thomas Nelson and Sons, New York (1954).
Descartes, Rene, (1641), MEDITATIONS ON FIRST PHILOSOPHY as reprinted by Thomas Nelson and Sons, New York (1954).
Einstein, Albert, (1916), The Foundation of the General Theory of Relativity, Annalen der Physik, 49, translated by W. Perrett and G. B. Jeffery in 1923, and published in THE PRINCIPLE OF RELATIVITY, Dover Publications, New York.
Goedel, Kurt, "On Formally Undecidable Propositions of Principia Mathematica and Related Systems", (1931).
Hamann, Jon Ray, MultiCoRelationalism see MultiCoRelationism (MCR): 2019
Heisenburg, Werner, THE PHYSICAL PRINCIPLES OF THE QUANTUM THEORY, translated by C. Eckart and C. Holt, University of Chicago Press, Chicago, (1930), Dover Publications, New York, (1949).
Jaynes, Edwin T., Phys. Rev., 106, p. 620; 108, p. 171, (1957). See also Jaynes and others in; Levine, R. D. and Tribus, M., editors, THE MAXIMUM ENTROPY FORMALISM, The MIT Press, (1979).
Laplace, Pierre Simon, Marquis de, THEORIE ANALYTIQUE DES PROBABILITIES, 3rd edition, (1820).
Leibniz, Gottfried Wilhelm, MONADOLOGY, (1714) in LEIBNIZ PHILOSOPHICLA WRITINGS, edited by G. H. R. Parkinson, translated by Mary Morris and G. H. R. Parkinson, J. M. Dent & Sons: London, (1973).
Peirce, Charles Sanders, see COLLECTED PAPERS OF CHARLES SANDERS PEIRCE, volumes 1 - 6 edited by C. Hartshorne and P. Weiss, (1931-1935). In particular see the Pragmatism Lectures at Harvard (1903) in vol. 5, pp. 14 - 212, and the articles on "What Pragmatism is" from The Monist (1905) in vol. 5 pp. 411 - 463. Perice’s thinking on discrete points in a continuum is presented in REASONING AND THE LOGIC OF THINGS, edited by Kenneth Laine Ketner, pg 159-160. This section is from the reprint of the third of his 1898 Harvard Lectures, “The Logic of Relatives”
Russell, Bertrand, "On Some Difficulties in the Theory of Transfinite Numbers and Order Types", Proc. London Math. Soc., ser. 2, 4, p.29, (1906).
Shannon, Claude, Bell System Tech. J., 27, p. 379, 623, (1948), reprinted in THE MATHEMATICAL THEORY OF COMMUNICATION, University of Illinois Press, Urbana (1949).