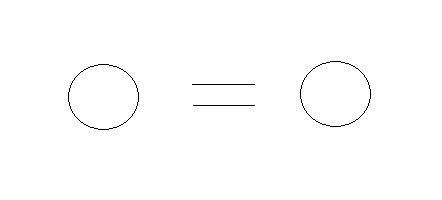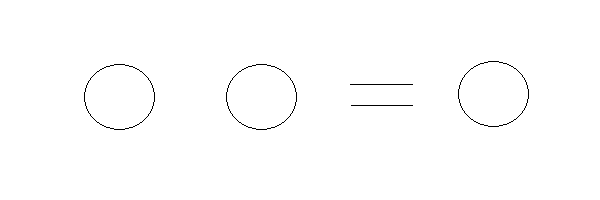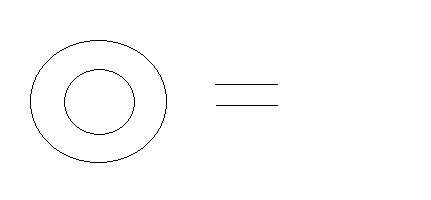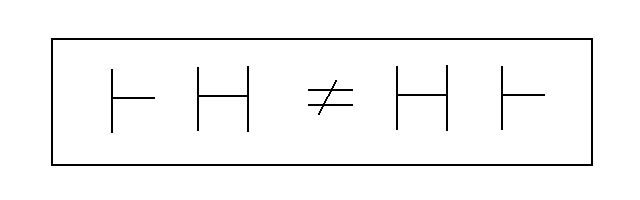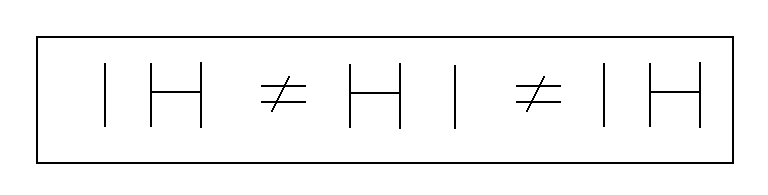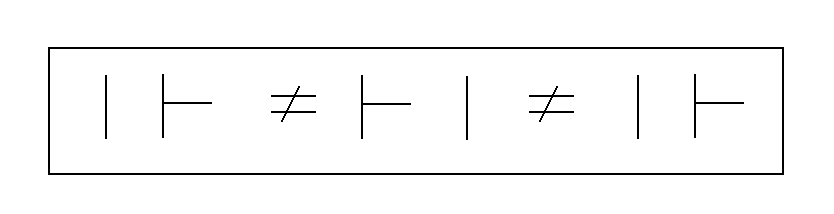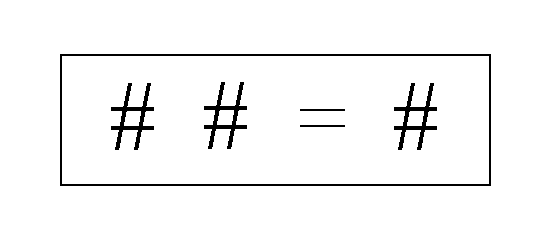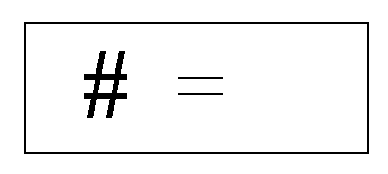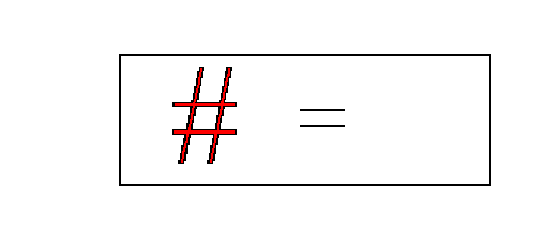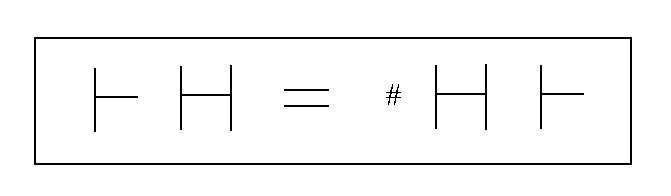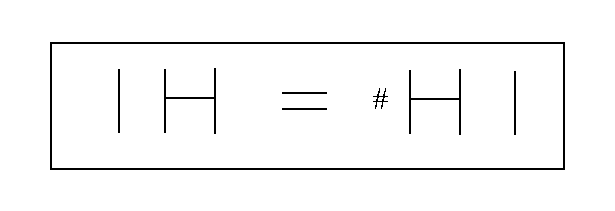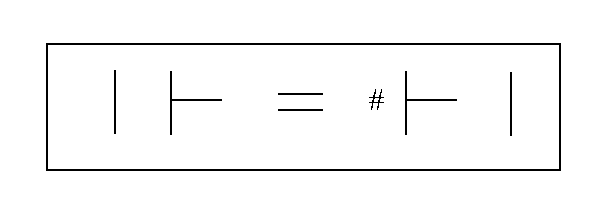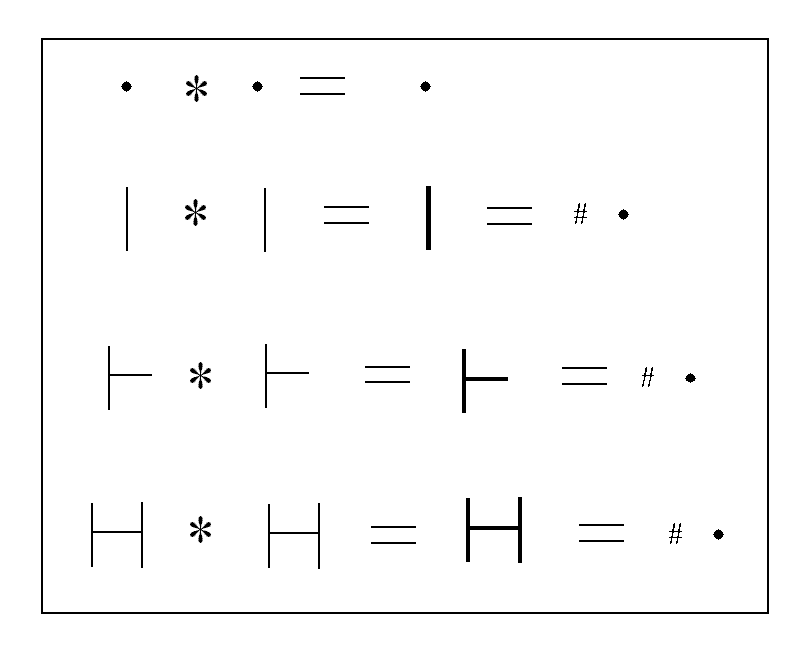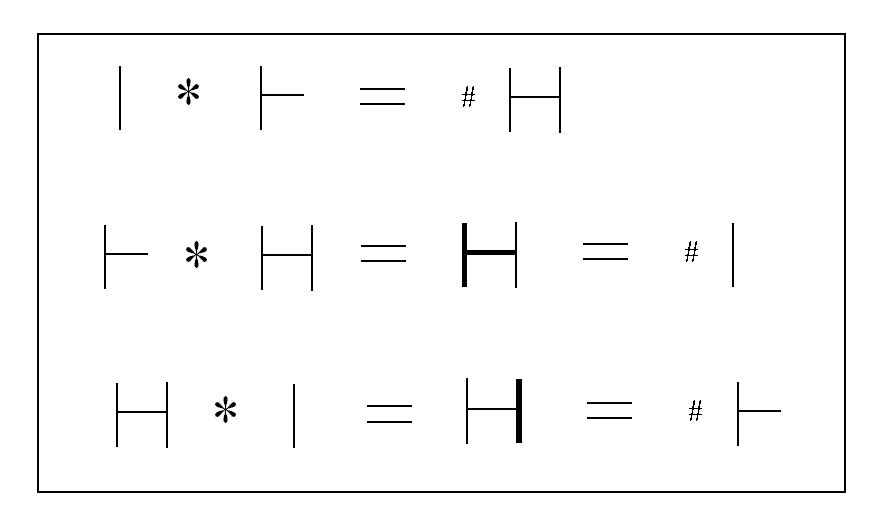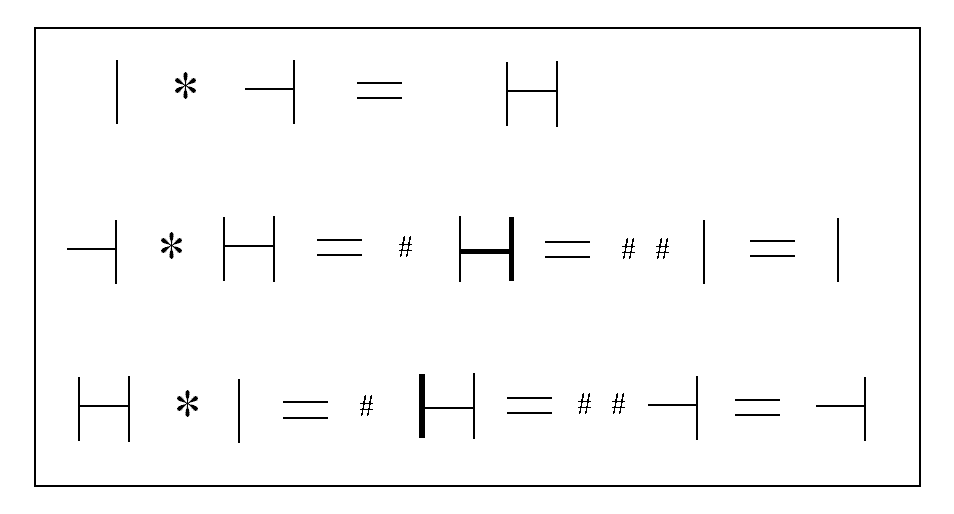Math & Science
Derivation of Mathematics
In The ODODU Language the initial mathematical concepts were presented in HVU form as;
HUU addition
HIU division
HEU multiplication
HAU subtraction
HOU association
HQU equivalence relation
HYU function
HHU equation
These are viewed as mathematical interpretations or aspects of the initiating eight vowels of ODODU;
UUU self relation
UIU linear relation
UEU relational relation
UAU interrelational relation
UOU distinction
UQU cross
UYU name, mark
UHU operation, interaction, interrelation
To the Top
The derivational arguments for these interpretations are as follows:
HUU addition: This is a relation which defines a new self. It is a relation which associates various components with each other to create a new self comprising those components and is thus a form of self relation. It is an embodiment of the concept of succession as it can be applied to numbers. Through the addition of one to a prior number a new number is created and this generates the Natural or counting numbers, and hence the integers once certain additional preliminaries have been established.
HIU division: This is a relation that describes parts of a whole or self. Hence it is a relation which partitions a whole into parts and is thus a relation between a whole and a part of a whole. This allows us to assign numbers to these parts and wholes and hence relates to the generation of the rational numbers or fractions.
HEU multiplication: This is a relation that defines a method of classifying which represents certain variables or numbers in terms of relationships between other variables or numbers. It represents a shortcut method for addition by classifying groups of numbers and then adding the groups. In this sense it is a relational relation. This leads to the derivations of exponents and logarithms and the generation of the real number system.
HAU subtraction: This is a relation that interrelates the relationships between and among various combinations of numbers and variables, and this allows us to remove some of them from consideration. Subtraction as a process then leads to a way of describing the result of such operations by creating the idea of a negative number. This allows us to remove more than we have and still have a vialbe descriptive system. Subtraction as a removal process generates the possibility of cancelation and this leads to the concept of zero. It allows all of the other number systems to expand by including negative numbers and it also leads to the generation of complex and hypercomplex numbers.
HOU association: This is a concept that emerges as a result of forming a distinction. It establishes a relation that allows for differentiation created by the distinction and an association of entities or numbers on one side of a distinction in contrast to those on the other side of the distinction..
HQU equivalence relation: Once a distinction or boundary has been created this relation allows for a crossing of that boundary or distinction. It establishes relationships across that boundary or allows for a comparison of what resides on each side of that boundary. Thus we can establish numbers as criteria of equalivance or difference of the components on either side with respect to some additional characteristics.
HYU function: Given a boundary and a cross, a mark of what is on one side of the boundary allows us to represent apsects of that side of the boundary that can then be compared with what may or may not be on the other side of the boundary. Functions can be converted to numbers in accordance with various criteria and this allows for their comparison with numbers.
HHU equation: These are relationships interconnecting the relationships between marks and their functions as crosses are made across a boundary. As such these interrelations become the basis for the ideas that constitute mathematics. They allow us to work with numbers in a way that can serve pragmatic purposes as we describe the universe and ourselves with language.
The HJU words were presented in The ODODU Language as:
HDU point
HPU line
HRU surface
HBU space, volume
HCU set
HLU equivalence relation
HTU redundancy
HKU combination/cancelation
HSU set of relations
HGU relational cross
HFU relational mark
HXU relational combination/cancelation
HNU element of a set
HMU association
HWU intersection
HZU union
HDU, HPU, HRU, and HBU are all geometrical concepts that are usually presented as axiomatic assumptions. We all have an intuitive understanding of what these concepts are and how they have developed from common experience. In ODODU we will not view these concepts as being subsumptively related. Thus a line is not composed of an infinite number of points. A surface is not composed of an infinite number of lines. A space or volume is not composed of an infinite number of surfaces.
To the Top
Like all mathematical concepts HDU, HPU, HRU, and HBU are ideas. As the initiating ideas for mathematics we consider that they generate a context or an idea space within which all other mathematical ideas can be conceived or considered. Call this the Mathematical Space. This is similar to the way that UIEA generates a concept of a real space which is and contains the universe and ourselves. Some additional derivational discussion of these concepts follows. In this discussion the HJU words will provide a general derivation and the HJV*U words will provide a fourfold perspective on each derivation. (V* are the U, I, E, and A vowels.)
HDU: point
HDUU: a point as origin
HDIU: a point on a line
HDEU: a point on a surface
HDAU: a point in space
HPU: line
HPUU: a closed line, a line which begins and terminates on itself such as a circle
HPIU: a line segment
HPEU: a line on a surface
HPAU: a line in space
HRU: surface
HRUU: a closed surface, a surface with no edges such as a sphere
HRIU: a cut through a surface, an edge or line resulting from such a cut
HREU: a section of a surface
HRAU: a surface in space
HBU: space, volume
HBUU: a space of origin
HBIU: a space intersecting a line, the line segment resulting from such an intersection
HBEU: a space intersecting a surface, the surface section resulting from such an intersection
HBAU: a space within another space, a subspace
HCU: Once we have the Mathematical Space as derived by the preceding words, the next defining event is the construction of the idea of a distinction or boundary. This we shall call a set. In its purest form it is a closed boundary within the Mathematical Space. In its first and simplest form it does not contain anything or do anything, it is just a boundary. Because it does not contain anything it will be designated as an empty set or the null set. Show it as;
HUU addition
HIU division
HEU multiplication
HAU subtraction
HOU association
HQU equivalence relation
HYU function
HHU equation
These are viewed as mathematical interpretations or aspects of the initiating eight vowels of ODODU;
UUU self relation
UIU linear relation
UEU relational relation
UAU interrelational relation
UOU distinction
UQU cross
UYU name, mark
UHU operation, interaction, interrelation
To the Top
The derivational arguments for these interpretations are as follows:
HUU addition: This is a relation which defines a new self. It is a relation which associates various components with each other to create a new self comprising those components and is thus a form of self relation. It is an embodiment of the concept of succession as it can be applied to numbers. Through the addition of one to a prior number a new number is created and this generates the Natural or counting numbers, and hence the integers once certain additional preliminaries have been established.
HIU division: This is a relation that describes parts of a whole or self. Hence it is a relation which partitions a whole into parts and is thus a relation between a whole and a part of a whole. This allows us to assign numbers to these parts and wholes and hence relates to the generation of the rational numbers or fractions.
HEU multiplication: This is a relation that defines a method of classifying which represents certain variables or numbers in terms of relationships between other variables or numbers. It represents a shortcut method for addition by classifying groups of numbers and then adding the groups. In this sense it is a relational relation. This leads to the derivations of exponents and logarithms and the generation of the real number system.
HAU subtraction: This is a relation that interrelates the relationships between and among various combinations of numbers and variables, and this allows us to remove some of them from consideration. Subtraction as a process then leads to a way of describing the result of such operations by creating the idea of a negative number. This allows us to remove more than we have and still have a vialbe descriptive system. Subtraction as a removal process generates the possibility of cancelation and this leads to the concept of zero. It allows all of the other number systems to expand by including negative numbers and it also leads to the generation of complex and hypercomplex numbers.
HOU association: This is a concept that emerges as a result of forming a distinction. It establishes a relation that allows for differentiation created by the distinction and an association of entities or numbers on one side of a distinction in contrast to those on the other side of the distinction..
HQU equivalence relation: Once a distinction or boundary has been created this relation allows for a crossing of that boundary or distinction. It establishes relationships across that boundary or allows for a comparison of what resides on each side of that boundary. Thus we can establish numbers as criteria of equalivance or difference of the components on either side with respect to some additional characteristics.
HYU function: Given a boundary and a cross, a mark of what is on one side of the boundary allows us to represent apsects of that side of the boundary that can then be compared with what may or may not be on the other side of the boundary. Functions can be converted to numbers in accordance with various criteria and this allows for their comparison with numbers.
HHU equation: These are relationships interconnecting the relationships between marks and their functions as crosses are made across a boundary. As such these interrelations become the basis for the ideas that constitute mathematics. They allow us to work with numbers in a way that can serve pragmatic purposes as we describe the universe and ourselves with language.
The HJU words were presented in The ODODU Language as:
HDU point
HPU line
HRU surface
HBU space, volume
HCU set
HLU equivalence relation
HTU redundancy
HKU combination/cancelation
HSU set of relations
HGU relational cross
HFU relational mark
HXU relational combination/cancelation
HNU element of a set
HMU association
HWU intersection
HZU union
HDU, HPU, HRU, and HBU are all geometrical concepts that are usually presented as axiomatic assumptions. We all have an intuitive understanding of what these concepts are and how they have developed from common experience. In ODODU we will not view these concepts as being subsumptively related. Thus a line is not composed of an infinite number of points. A surface is not composed of an infinite number of lines. A space or volume is not composed of an infinite number of surfaces.
To the Top
Like all mathematical concepts HDU, HPU, HRU, and HBU are ideas. As the initiating ideas for mathematics we consider that they generate a context or an idea space within which all other mathematical ideas can be conceived or considered. Call this the Mathematical Space. This is similar to the way that UIEA generates a concept of a real space which is and contains the universe and ourselves. Some additional derivational discussion of these concepts follows. In this discussion the HJU words will provide a general derivation and the HJV*U words will provide a fourfold perspective on each derivation. (V* are the U, I, E, and A vowels.)
HDU: point
HDUU: a point as origin
HDIU: a point on a line
HDEU: a point on a surface
HDAU: a point in space
HPU: line
HPUU: a closed line, a line which begins and terminates on itself such as a circle
HPIU: a line segment
HPEU: a line on a surface
HPAU: a line in space
HRU: surface
HRUU: a closed surface, a surface with no edges such as a sphere
HRIU: a cut through a surface, an edge or line resulting from such a cut
HREU: a section of a surface
HRAU: a surface in space
HBU: space, volume
HBUU: a space of origin
HBIU: a space intersecting a line, the line segment resulting from such an intersection
HBEU: a space intersecting a surface, the surface section resulting from such an intersection
HBAU: a space within another space, a subspace
HCU: Once we have the Mathematical Space as derived by the preceding words, the next defining event is the construction of the idea of a distinction or boundary. This we shall call a set. In its purest form it is a closed boundary within the Mathematical Space. In its first and simplest form it does not contain anything or do anything, it is just a boundary. Because it does not contain anything it will be designated as an empty set or the null set. Show it as;
HCUU: The null set as a concept. The concept of nothing or no thing.
HCIU: The boundary of a null set.
HCEU: The representation of the null set.
HCAU: The interrelation of the concept of the null set to the concepts that generate the Mathematical Space
HLU: Given one null set, HCU, and then constructing a second null set doesn't change what we have. The two null sets are equivalent and having two or more null sets doesn't generate a new idea. All null sets are the same or equivalent. Show this as;
HCIU: The boundary of a null set.
HCEU: The representation of the null set.
HCAU: The interrelation of the concept of the null set to the concepts that generate the Mathematical Space
HLU: Given one null set, HCU, and then constructing a second null set doesn't change what we have. The two null sets are equivalent and having two or more null sets doesn't generate a new idea. All null sets are the same or equivalent. Show this as;
HLUU: The origin of equivalence.
HLIU: The equivalence relation.
HLEU: The representation of the equivalence relation.
HLAU: The use of the equivalence relation within the mathematical space.
HTU: Establishing that all null sets are equivalent generates the additional concept of redundancy. Thus if one null set is equivalent to another null set, then two null sets are also equivalent to another null set. Call this the law of redundancy and show it as
HLIU: The equivalence relation.
HLEU: The representation of the equivalence relation.
HLAU: The use of the equivalence relation within the mathematical space.
HTU: Establishing that all null sets are equivalent generates the additional concept of redundancy. Thus if one null set is equivalent to another null set, then two null sets are also equivalent to another null set. Call this the law of redundancy and show it as
HTUU: The origin of redundancy.
HTIU: The redundancy relation.
HTEU: The representation of the redundancy relation.
HTAU: The use of the redundancy relation within the Mathematical Space.
HKU: We now introduce the concept of combining null sets. This actually doesn't make any sense since putting anything into a null set means that it no longer is a null set. So putting a null set into a null set can be viewed as eliminating or cancelling the null set, or both null sets since they are equivalent. This can also be viewed as superimposing one null set over another null set. Call this the law of combination/cancellation and show it as
HKUU: The origin of cancelation.
HKIU: The cancelation relation.
HKEU: The representation of the cancelation relation.
HKAU: The use of the cancelation relation within the Mathematical Space
These last four HJU words and their HJV*V extensions can now be seen to be similar to the initial development that George Spencer Brown presented in "Laws of Form". The difference is that here we have first derived a Mathematical Space which is an idea space within language and then introduced an initial formation of a boundary as distinguishing nothing. This we have called the null or empty set. Relative to the null set we have constructed concepts of equivalence, redundancy and cancellation.
The next step is to start putting something (ideas) into a boundary which has been derived as a null set. When we do this it is no longer an empty set but becomes what we shall call a Regular Set. It now becomes a boundary which contains or separates something from the rest of the Mathematical Space which contained the initial null set. The defining boundaries of these Regular Sets (just sets from now on) will themselves be subject to the same rules of equivalency, redundancy, and cancellation that we applied to the null set. In general the contents of sets will not follow these rules.
As we derive the next eight HJU words we will do so within the context of the Mathematical Space, sets, and their rules, as presented in the first eight HJU words. The result will generate a structure that will resemble, and perhaps actually be, what we usually call mathematics. All the HJU words will provide an outline of this argument and the HJV*U words will then fill out the derivation. (V* are the U, I, E, and A vowels.)
The derivations of these HJU words are presented and illustrated in conjunction with the corresponding HJV*U words as follows:
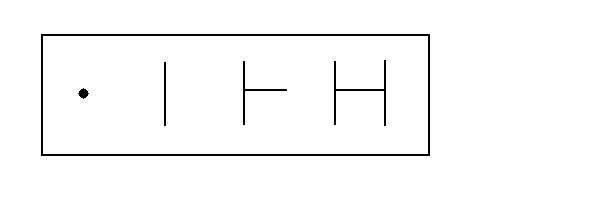
HSU: The first ideas we can put into a null set boundary will be the initiating relations which began this whole derivation. In keeping with the understanding that relation is really four relations, or four dimensional, or has four integral components, it is necessary to start with the whole of relation. This means that all four of the initiating UIEA relations become the first entry into the set concept boundary as we start the derivation of mathematics. Thus HSU is:
HKIU: The cancelation relation.
HKEU: The representation of the cancelation relation.
HKAU: The use of the cancelation relation within the Mathematical Space
These last four HJU words and their HJV*V extensions can now be seen to be similar to the initial development that George Spencer Brown presented in "Laws of Form". The difference is that here we have first derived a Mathematical Space which is an idea space within language and then introduced an initial formation of a boundary as distinguishing nothing. This we have called the null or empty set. Relative to the null set we have constructed concepts of equivalence, redundancy and cancellation.
The next step is to start putting something (ideas) into a boundary which has been derived as a null set. When we do this it is no longer an empty set but becomes what we shall call a Regular Set. It now becomes a boundary which contains or separates something from the rest of the Mathematical Space which contained the initial null set. The defining boundaries of these Regular Sets (just sets from now on) will themselves be subject to the same rules of equivalency, redundancy, and cancellation that we applied to the null set. In general the contents of sets will not follow these rules.
As we derive the next eight HJU words we will do so within the context of the Mathematical Space, sets, and their rules, as presented in the first eight HJU words. The result will generate a structure that will resemble, and perhaps actually be, what we usually call mathematics. All the HJU words will provide an outline of this argument and the HJV*U words will then fill out the derivation. (V* are the U, I, E, and A vowels.)
The derivations of these HJU words are presented and illustrated in conjunction with the corresponding HJV*U words as follows:
HSU: The first ideas we can put into a null set boundary will be the initiating relations which began this whole derivation. In keeping with the understanding that relation is really four relations, or four dimensional, or has four integral components, it is necessary to start with the whole of relation. This means that all four of the initiating UIEA relations become the first entry into the set concept boundary as we start the derivation of mathematics. Thus HSU is:
Here the rectangular boundary denotes the relational set, which is a set within Mathematical Space, and the UIEA pictographs denote the relations of the relational set. Hence;
HSU: The Relational Set
HSUU: the U relation (UUU) of the Relational Set
HSIU: the I relation (UIU) of the Relational Set
HSEU: the E relation (UEU) of the Relational Set
HSAU: the A relation (UAU) of the Relational Set
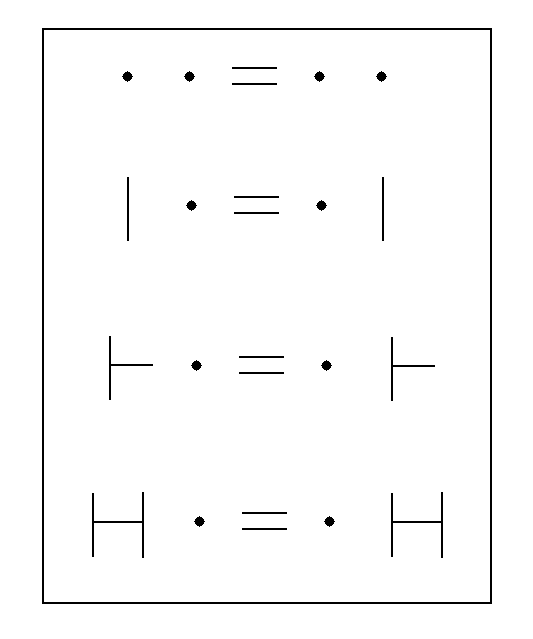
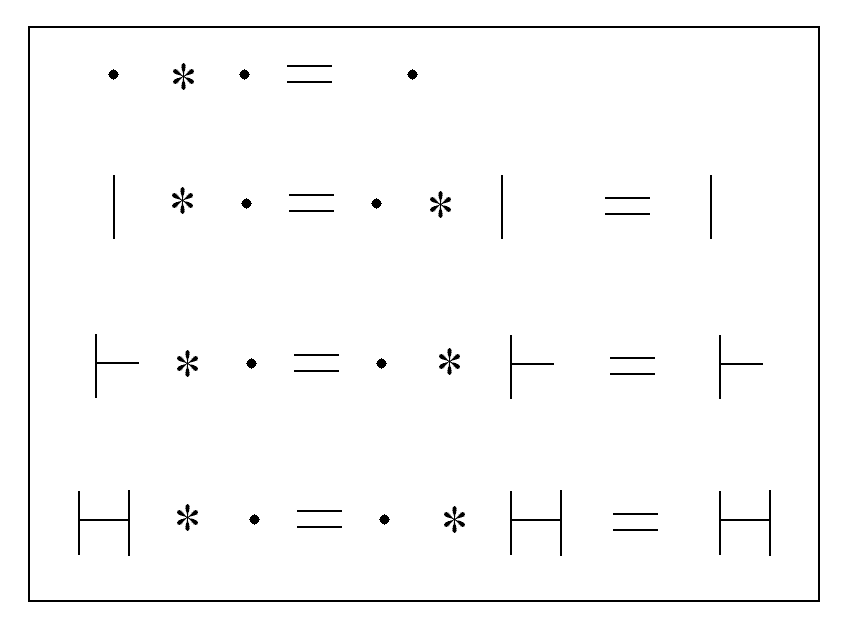
HGU: The Relational Cross. This describes how relations in the Relational Set can cross each other within the Relational Set. The cross is just what it implies. Given the symbols for two relations (we represent the relations by their symbols) we perform a cross by moving one of the symbols through the other symbol until it is on the other side of that symbol. This occurs within the Mathematical Space we have just derived.
HGUU: the U or unitary cross. This includes all crosses which involve the U relation as follows
HSU: The Relational Set
HSUU: the U relation (UUU) of the Relational Set
HSIU: the I relation (UIU) of the Relational Set
HSEU: the E relation (UEU) of the Relational Set
HSAU: the A relation (UAU) of the Relational Set
HGU: The Relational Cross. This describes how relations in the Relational Set can cross each other within the Relational Set. The cross is just what it implies. Given the symbols for two relations (we represent the relations by their symbols) we perform a cross by moving one of the symbols through the other symbol until it is on the other side of that symbol. This occurs within the Mathematical Space we have just derived.
HGUU: the U or unitary cross. This includes all crosses which involve the U relation as follows
We use the = sign in these representations to mean that the meaning of the pair of relations, say U and E, when presented as UE, is the same as presenting it as EU.
HGIU: This is the I cross and it involves the case when E crosses H or H crosses E. The I cross does not actually involve I itself in the cross. It is represented as
Note that in this case we are saying that for the relations E and A that the presentation EA does not mean the same as AE. This is symbolized with the use of the "not equals" sign.
HGEU: This is the E cross and it involves the case when I crosses H or when H crosses I. It is represented as
HGEU: This is the E cross and it involves the case when I crosses H or when H crosses I. It is represented as
HGAU: This is the A cross and it involves the case where I crosses H or when H crosses I. It is represented as
Note that in the three crosses HGIU, HGEU, and HGAU that the result is not commutative. Thus if you start with an I and E relational pair, and the I then crosses the E, that the meaning of the resulting E and I pair is not the same as the meaning of the original I and E pair. This contrasts with the situation in HGUU where the U relation can cross with any other relation and the resulting pair will have the same meaning as the original pair. The U relation crosses commutatively with any other relation whereas the other relations do not cross commutatively with each other.
HFU: The Relational Mark. This describes how we can mark or distinguish when a Relational Cross has occurred. The Relational Mark makes a distinction and it therefore behaves like our initial distinction in the Mathematical Space which was the set. The Relational Mark will be symbolized with a # sign. This # sign is the one additional feature within a set which will follow the rules which we have derived for the set defining boundary itself. See HPU, HRU, and HBU above. As was the case for sets, to make a mark, and then make another mark, is the same as making only one mark. Thus
HFU: The Relational Mark. This describes how we can mark or distinguish when a Relational Cross has occurred. The Relational Mark makes a distinction and it therefore behaves like our initial distinction in the Mathematical Space which was the set. The Relational Mark will be symbolized with a # sign. This # sign is the one additional feature within a set which will follow the rules which we have derived for the set defining boundary itself. See HPU, HRU, and HBU above. As was the case for sets, to make a mark, and then make another mark, is the same as making only one mark. Thus
But when two marks are combined they superimpose themselves over each other and cancel each other out. We are left with nothing or no mark at all. In this case we do a cross and mark it, and then do another cross and mark that. The second mark marks the first mark and they cancel each other out. Thus;
This could also be shown as
Where the mark for a second cross would be shown in red.
The Relational Marks apply to the Relational Crosses as follows;
HFUU: Since all HGUU unitary crosses are equal there is no reason to make a mark. Therefore the Relational Mark HFUU is not used for unitary crosses.
HFIU: The Relational Mark applied to the I Relational Cross is as follows
The Relational Marks apply to the Relational Crosses as follows;
HFUU: Since all HGUU unitary crosses are equal there is no reason to make a mark. Therefore the Relational Mark HFUU is not used for unitary crosses.
HFIU: The Relational Mark applied to the I Relational Cross is as follows
This contrasts with the situation in HGIU where the E and A relational cross was not commutative. By introducing the mark # to designate a cross the meaning of the two pairs (E & A) and (#A & E) is the same. Thus the meaning of #AE is the same as the meaning of EA after the E has crossed the A. This applies to the following two marked crosses as well.
HFEU: The Relational Mark applied to the E Relational Cross is as follows:
HFEU: The Relational Mark applied to the E Relational Cross is as follows:
HFAU: The Relational Mark applied to the A Relational Cross is as follows:
HXU: When two relations within the Relational Set cross each other an interaction can occur and this is called the combination/cancellation interaction. This interaction acts like a mathematical binary operation and must result in a valid relation of the Relational Set. The combination/cancellation interaction will be represented by the symbol * and it is defined as a binary operation as follows:
HXUU: This defines how the U relation interacts with the relations of the Relational Set under the * operation
HXIU: This defines how the * operation acts when a relation is operated on itself:
In this case when the I, E, and A relations are combined with the binary operation * they superimpose on each other and cancel each other out. This is shown in the pictograph as first making a darker, larger symbol, and then setting this equal to a marked U relation. The interpretation that the relational superposition and cancellation does not lead to nothing, as was the case for sets and marks, is one of the defining characteristics of the * operation. Thus a relational cross leads to a marked result, and a relational combination/cancellation under the binary operation * leads to a marked unitary relation, U.
HXEU: This defines how the * binary operation functions when one or both of the relations involved is marked. Thus;
When the * binary operation operates on a marked and an unmarked relation, the result is always a marked relation.
When the * binary operation operates on two marked relations the result is always an unmarked relation.
HXAU: This defines how the * binary operation functions when the two interacting relations are different from each other and neither is the U relation.
HXEU: This defines how the * binary operation functions when one or both of the relations involved is marked. Thus;
When the * binary operation operates on a marked and an unmarked relation, the result is always a marked relation.
When the * binary operation operates on two marked relations the result is always an unmarked relation.
HXAU: This defines how the * binary operation functions when the two interacting relations are different from each other and neither is the U relation.
In the first of these three operations the mark is due to the cross. In the last two of these operations the mark is due to the superposition of one of the relations on or over part of the other relation and the cancellation of the superimposed part (represented by the darker lines above) resulting in a valid relation.
It is interesting and relevant to note that if we rotate the four relational pictographs by 180 degrees that the rotated pictographs for U, I, and A are indistinguishable from the non rotated symbols. However, this is not the case with E which therefore has a right handed representation or a left handed representation. This actually has meaning in the HXAU derivations. If we call the E relation pictograph we have been using so far as right handed, then we can represent a left handed E as E' and illustrate it with the alternative pictographic symbol of
It is interesting and relevant to note that if we rotate the four relational pictographs by 180 degrees that the rotated pictographs for U, I, and A are indistinguishable from the non rotated symbols. However, this is not the case with E which therefore has a right handed representation or a left handed representation. This actually has meaning in the HXAU derivations. If we call the E relation pictograph we have been using so far as right handed, then we can represent a left handed E as E' and illustrate it with the alternative pictographic symbol of
We then get an alternative interpretation of HXAU, as follows
In the first case of this alternative interpretation there is no cross and no cancellation so the result is simply that I * E' = A.
In the second case E' first crosses A and this generates a mark #. After this cross all of E' superimposes on part of A and this leads to a second mark and the cancellation of the superimposed part of A. The result is a double marked I and this is equivalent to an unmarked I.
In the third case H crosses I and this generates a mark. Note that H cannot just interact with I to produce E, as I and E' interacted to produce A in the first case, because the result would be a right handed E and this is an HXAU with only left handed E' relations. So H has to fully cross I and thus generate a mark. The I then superimposes on the left hand part of the A and this generates a cancellation of the superimposed part, and generates another mark. Thus we have a double marked left handed E' and this in turn is equal to an unmarked E'.
Using a left handed E' does not change the results of HXUU, HXIU and HXEU in any way other than the E' is left handed instead of right handed. The results of the operations are the same.
Thus there are two possibilities for HXU, one which has a marked E' in HXAU and one which has an unmarked E in HXAU. The difference is significant and will be discussed later.
Continuing with the derivation of the mathematical concept words:
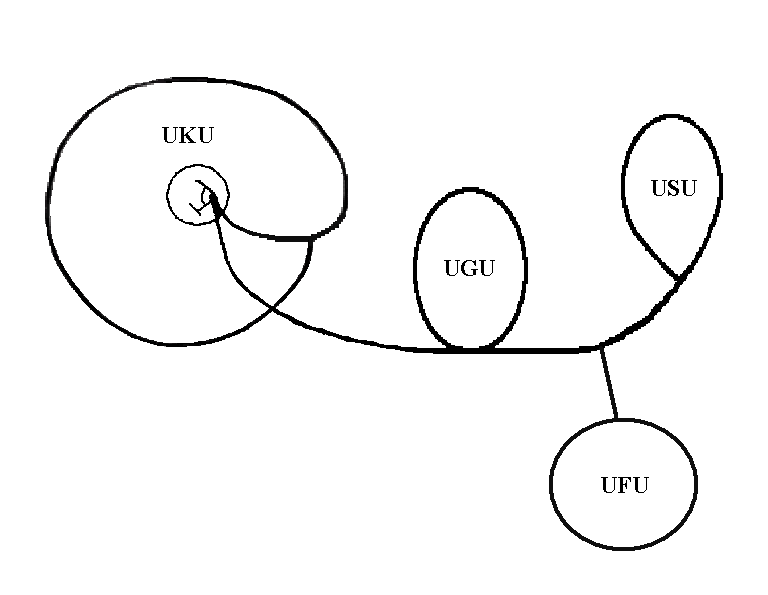
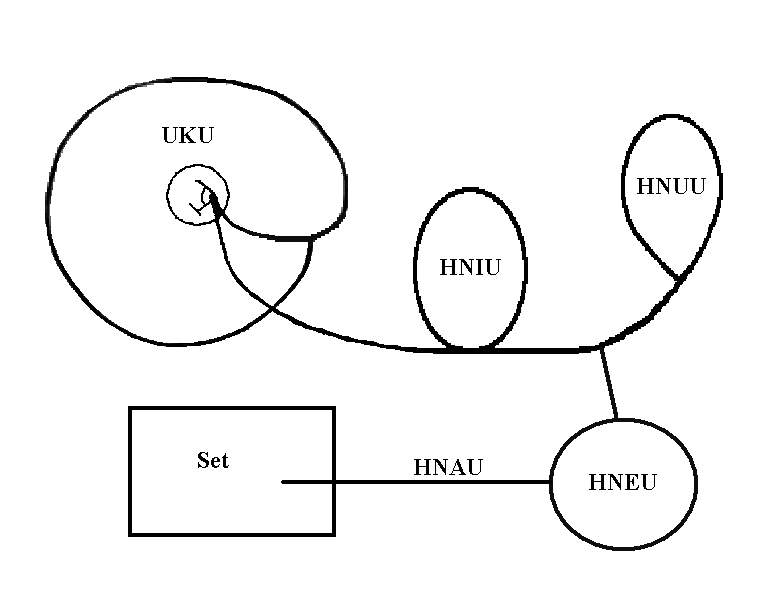
HNU: An element or member of a set. This concept applies when we consider putting anything other than relation into an empty set. This will now be the meaning of the word set from here on and thus is distinguished from the empty set and the Relational Set. We will derive it as a set containing elements as follows. Remember the derivation of UFU in The Derivation of Archetypal Meaning in ODODU. We can label the components of this derivation as:
In the second case E' first crosses A and this generates a mark #. After this cross all of E' superimposes on part of A and this leads to a second mark and the cancellation of the superimposed part of A. The result is a double marked I and this is equivalent to an unmarked I.
In the third case H crosses I and this generates a mark. Note that H cannot just interact with I to produce E, as I and E' interacted to produce A in the first case, because the result would be a right handed E and this is an HXAU with only left handed E' relations. So H has to fully cross I and thus generate a mark. The I then superimposes on the left hand part of the A and this generates a cancellation of the superimposed part, and generates another mark. Thus we have a double marked left handed E' and this in turn is equal to an unmarked E'.
Using a left handed E' does not change the results of HXUU, HXIU and HXEU in any way other than the E' is left handed instead of right handed. The results of the operations are the same.
Thus there are two possibilities for HXU, one which has a marked E' in HXAU and one which has an unmarked E in HXAU. The difference is significant and will be discussed later.
Continuing with the derivation of the mathematical concept words:
HNU: An element or member of a set. This concept applies when we consider putting anything other than relation into an empty set. This will now be the meaning of the word set from here on and thus is distinguished from the empty set and the Relational Set. We will derive it as a set containing elements as follows. Remember the derivation of UFU in The Derivation of Archetypal Meaning in ODODU. We can label the components of this derivation as:
Add a set to this pictograph and relabel it as follows;
Thus we now have;
HNU: An element or member of a set. This element is derived by the preceding pictograph, where;
HNUU: Is the symbol for the element of the set.
HNIU: Is the description of the element of the set.
HNEU: Is the image of the element of the set.
HNAU: Is the membership relation by which the element of the set is established or derived as an element of the set.
HMU: An association of elements of a set.
HMUU: The symbol or name of the association of elements of a set.
HMIU: A connecting relation for all elements of an association, relating each of them to all the other elements of the association and not to any other elements of the set.
HMEU: An identifying mark, such as ( ). which defines or illustrates an association within a set such that elements of the association can be clearly distinguished from all other elements of the set.
HMAU: The inclusion of an association of elements in a set as being itself a member of the set. This will now be defined as a subset of the set. Thus an association of elements of a set, which is by definition a subset of the set, is itself a member or element of the set. By also including all associations of a single element (an element associated with itself) as subsets of the set, as well as the empty set and the set itself, we have completed the derivation of the set concept.
We continue with the derivation of two operations on sets as follows; First
HWU: This is a binary operation called intersection which is defined for any two subsets of a set such that the operation meets the following criteria.
HWUU: The intersection operation will be identified by the symbol
HNU: An element or member of a set. This element is derived by the preceding pictograph, where;
HNUU: Is the symbol for the element of the set.
HNIU: Is the description of the element of the set.
HNEU: Is the image of the element of the set.
HNAU: Is the membership relation by which the element of the set is established or derived as an element of the set.
HMU: An association of elements of a set.
HMUU: The symbol or name of the association of elements of a set.
HMIU: A connecting relation for all elements of an association, relating each of them to all the other elements of the association and not to any other elements of the set.
HMEU: An identifying mark, such as ( ). which defines or illustrates an association within a set such that elements of the association can be clearly distinguished from all other elements of the set.
HMAU: The inclusion of an association of elements in a set as being itself a member of the set. This will now be defined as a subset of the set. Thus an association of elements of a set, which is by definition a subset of the set, is itself a member or element of the set. By also including all associations of a single element (an element associated with itself) as subsets of the set, as well as the empty set and the set itself, we have completed the derivation of the set concept.
We continue with the derivation of two operations on sets as follows; First
HWU: This is a binary operation called intersection which is defined for any two subsets of a set such that the operation meets the following criteria.
HWUU: The intersection operation will be identified by the symbol
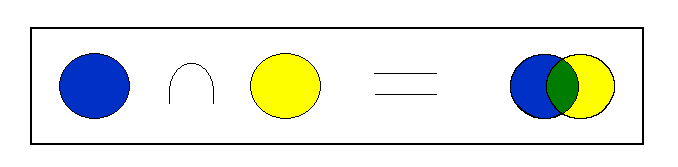
HWIU: Relative to any two subsets of a set the intersection operation will define a new or additional subset which contains only those elements which are in both of the given two subsets.
HWEU: A pictographic image of the intersection operation is
HWEU: A pictographic image of the intersection operation is
Where the green identifies the subset resulting from the intersection operation on the blue and yellow subsets.
HWAU: The inclusion of the intersection operation as an essential part, process, or law defined on all sets.
The second operation is;
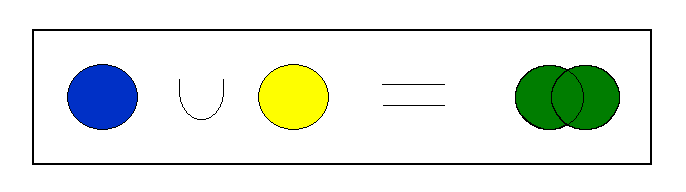
HZU: This is a binary operation called union which is defined for any two subsets of a set such that the operation meets the following criteria.
HZUU: The union binary operation will be identified by the symbol
HWAU: The inclusion of the intersection operation as an essential part, process, or law defined on all sets.
The second operation is;
HZU: This is a binary operation called union which is defined for any two subsets of a set such that the operation meets the following criteria.
HZUU: The union binary operation will be identified by the symbol
HZIU: Relative to any two subsets of a set the intersection operation will define a new or additional subset which contains any element which is in either of the given two subsets, or is in both of the given two subsets.
HZEU: A pictographic image of the union binary operation is
HZEU: A pictographic image of the union binary operation is
Where the green identifies the subset resulting from the union operation on the blue and yellow subsets.
HZAU: The inclusion of the union operation as an essential part, process, or law defined on all sets
HZAU: The inclusion of the union operation as an essential part, process, or law defined on all sets